|
|
 |
| |
Концепция перспективной многоразовой
аэрокосмической транспортной системы |
| Ю. И. Лобановский |
Lobanovsky Yu. I. Concept of an advanced reusable aerospace transportation system.
La Recherché Aerospatiale, 1996, no 2, 75-83. |
| |
Краткое содержание |
| В работе предлагаются концепция полностью многоразового двухступенчатого аэрокосмического самолета и новые решения в гиперзвуковой аэродинамике и схемах воздушно-реактивных двигателей. Эти инновации могут существенно увеличить эффективность аэрокосмического самолета как транспортного средства. Предложено также использовать дозвуковой самолет-заправщик для разрешения противоречия между гибкостью и эффективностью исследуемых аэрокосмических транспортных систем. |
| Рассматриваемая космическая транспортная система Star Liner, состоящая из полностью многоразового двухступенчатого аэрокосмического самолета и, в случае необходимости, дозвукового самолета-заправщика, позволяет, по предварительным оценкам, выводить на низкую околоземную орбиту полезные нагрузки, составляющие 8 - 12 % от стартовой массы аэрокосмического самолета при дальности полета на параллакс 3000 - 6500 км. Следовательно, относительная масса ее полезной нагрузки в 5 - 10 раз больше, чем у других известных полностью многоразовых космических транспортных систем, таких как Sänger или Delta Clipper. |
| Ключевые слова: Аэрокосмический самолет - Гиперзвуковые скорости - Аэрокосмическая транспортная система - Воздушно-реактивный двигатель - Ракетный двигатель - ГПВРД. |
| |
ТАБЛИЦА СИМВОЛОВ |
- M - число Маха
- Re - число Рейнольдса
- z - число Циолковского
- R0 - радиус полета на параллакс
- S0 - характерная дальность полета
- S - длина участка траектории
- s - безразмерная длина участка траектории
- Isp - удельный импульс
- U - характеристическая скорость
- V - скорость полета
- h - высота траектории
- g - ускорение свободного падения
- E - удельная энергия аппарата (E = 0.5V2 + gh)
- m - масса
- mF - масса топлива
- m(s) - относительная масса конструкции (доля сухой массы в стартовой массе аппарата)
- G - вес
- T - тяга
- L - подъемная сила
- D - сопротивление
- L/D - аэродинамическое качество
- η - пропульсивный коэффициент полезного действия
- Q - теплотворная способность топлива
- f - относительная масса топлива
- n - нормальная перегрузка ( n = L/mg )
- q - скоростной напор
- CL - коэффициент подъемной силы
- CD - коэффициент сопротивления
- W - характерная площадь крыла
- ν - объем корпуса
- τ - коэффициент объема (τ = ν 2/3/ W)
- θ - угол наклона траектории
- Ψ - угол разворота на вираже
- ε - увеличение угла наклона траектории при кабрировании
- k - параметр, характеризующий индивидуальные отклонения от характеристик двигателя от некоторой типовой кривой
- σ S - безразмерный параметр, описывающий летные данные по отношению к данным аэрокосмического самолета Sänger
- pi - безразмерные параметры
- ψ = T/D - 1
- Δe = ΔE/ηQ
- R = ηQ(L/D)/g
- ξ = (1 - V2/VE2)-1
- ω = CL/CLopt
|
| Индексы |
- c - крейсерский полет
- a - разгон
- t - разворот
- p - кабрирование
- g - планирование
- E - низкая околоземная орбита
- S - относится к характеристикам аппарата Sänger
|
| |
I - ВВЕДЕНИЕ |
| Эффективность многоразовой аэрокосмической транспортной системы для заданного класса аппаратов в первом приближении определяется отношением массы полезной нагрузки, выводимой на околоземную орбиту, к стартовой массе носителя. Гибкость ее применения обусловлена максимальным радиусом полета на параллакс. Качественный анализ характеристик всевозможных вариантов многоразовых носителей, использующих химическую энергию, позволил выделить три потенциально наиболее эффективных класса аппаратов. К ним относятся одноступенчатый аэрокосмический самолет типа NASP [1], одноступенчатый ракетный баллистический носитель типа Delta Clipper [2] и двухступенчатый аэрокосмический самолет типа Sänger [3]. |
| При этом близкие величины относительной полезной нагрузки - около 1 - 2 % от стартовой массы для аппаратов типа Sänger и Delta Clipper достигаются принципиально разными путями. Относительная масса конструкции m(s) аэрокосмического самолета Sänger составит около 0.49 - 0.50 от его стартовой массы [3] по сравнению со значением примерно 0.08 для водородно-кислородного ракетного аппарата Delta Clipper [2]. В то же время значительно большая эффективность воздушно-реактивной силовой установки, используемой на первой ступени аэрокосмического самолета, приводит к уменьшению полного расхода топлива на орбитальную транспортную операцию до 0.49 от стартовой массы носителя в первом случае [3] по сравнению с величиной 0.90 - 0.91 - во втором [2]. |
| Аэрокосмический самолет имеет абсолютное превосходство перед многоразовым носителем, использующим только ракетные двигатели, с точки зрения гибкости применения. Кроме того, даже если разработчикам аппаратов типа Delta Clipper и удастся создать конструкцию необходимого уровня совершенства, ресурсы для дальнейшего развития будут практически исчерпаны. В то же время, как показано далее, транспортная система на основе двухступенчатого аэрокосмического самолета может быть значительно эффективнее аппарата типа Sänger. |
| С учетом существенно бoльших аэродинамических потерь при разгоне носителей с воздушно-реактивными двигателями в зависимости от предполагаемого уровня технического совершенства перспективных гиперзвуковых прямоточных воздушно-реактивных двигателей, их применение может быть целесообразно до скоростей полета, соответствующих M = 12 - 15 [4,5]. Исследования в рамках программы NASP позволяют сделать вывод о том, что до этих скоростей возможен достаточно эффективный полет в атмосфере. Принимая в качестве ограничения нижнее значение числа Маха (M = 12 - 12.5) из указанного интервала, проведем анализ рационального сочетания авиационных и ракетных элементов многоразовых аэрокосмических носителей. Рассмотрим также влияние некоторых новых решений в гиперзвуковой аэродинамике и схемах воздушно-реактивных двигателей на эффективность подобных транспортных систем. |
| Относительная масса конструкции m(s) аэрокосмического самолета в настоящее время является, по-видимому, наиболее неопределенной величиной, изменяющейся в различных разработках от значений m(s) ≈ 0.50 для аппарата Sänger, до m(s) ≈ 0.20 - 0.25 в проекте европейского одноступенчатого носителя [5]. В качестве базовой точки в проводимом анализе примем соответствующие характеристики аэрокосмического самолета Sänger, как наиболее реалистичные. Ориентируясь на несколько более высокий технологический уровень, в дальнейшем будем считать, что относительная масса конструкции у первых ступеней рассматриваемых носителей, несмотря на увеличение максимальной скорости полета, такая же, как у первой ступени АКС Sänger или на 10 % больше. Для баллистических объектов базовая точка - аппарат Delta Clipper с минимальным возрастанием относительной массы конструкции на 25 % вследствие уменьшения масштаба [6]. |
| Важнейшим параметром аэрокосмического самолета является скорость, при которой происходит разделение ступеней у двухступенчатого варианта или переключение силовой установки на ракетный режим у одноступенчатого. Скорость разделения, характерная для аппарата типа Sänger и соответствующая числу Маха M = 6.5 - 7, является приемлемым компромиссом, не предъявляющим чрезмерно высоких требований как к первой, так и ко второй ракетной ступеням аэрокосмического самолета, и позволяющим использовать обе ступени в достаточно благоприятных для них условиях. Однако в этом случае на вторую, ракетную ступень, двигатели которой обладают относительно низким удельным импульсом (Isp = 4.65 - 4.7 км/с), приходится слишком большой участок разгонной траектории (характеристическая скорость U = 5.4 - 5.8 км/с). Поэтому отношение конечной массы второй ракетной ступени me к ее стартовой массе m2, обозначаемое z-1 = me/m2, где z - число Циолковского, составит величину не более 0.3. |
| Относительная масса конструкции многоразовой второй крылатой ракетной ступени соответствующего размера, используемой в концепции Sänger, по статистическим данным будет находиться в диапазоне от 0.20 до 0.25 [3,6] в зависимости от уровня ее технического совершенства, а также от того, является ли она автоматической или пилотируемой. Таким образом, если учесть запасы топлива для возвращения с орбиты, доля полезной нагрузки двухступенчатого аэрокосмического самолета типа Sänger составит приблизительно 0.03 - 0.08 от стартовой массы его второй ракетной ступени. Для обеспечения полета на параллакс радиусом R0 = 3000 км [7], что дает возможность выводить полезные нагрузки на орбиты с наклонением на 27° меньше, чем географическая широта стартовой позиции, отношение стартовых масс первой и второй ступеней m1/m2 аппарата Sänger составляет примерно 2.25 [3,6]. Следовательно, на орбиту может быть выведено не более 1 - 2.5 % от стартовой массы двухступенчатого аэрокосмического самолета рассматриваемой схемы. |
| Из анализа проблем аэротермодинамики [8], а также результатов исследования характеристик перспективных силовых установок [4,9], был сделан вывод о том, что при указанном выше ограничении скорости полета, соответствующем M < 12 - 12.5, достигается еще одна выделенная по технологическим условиям точка разгонной траектории, в которой целесообразно рассмотреть разделение ступеней двухступенчатого аэрокосмического самолета. Значительное уменьшение характеристической скорости второй ступени (U = 3.35 - 3.8 км/с) приводит к тому, что соотношение ее конечной и стартовой масс составит z-1 = 0.45 - 0.5. |
| Далее, для реализации потенциальных преимуществ ракетной ступени следует минимизировать массу ее конструкции. Очевидным решением является использование баллистической многоразовой верхней ступени типа аэрокосмического аппарата Delta Clipper, также совершающей вертикальную посадку с финальным гашением скорости при помощи двигателей. Затраты топлива на возвращение оценим величиной 0.1 от орбитальной массы второй ступени. В этом случае при относительной массе ее конструкции около 0.1, выводимая на орбиту полезная нагрузка составит примерно 0.3 - 0.4 от стартовой массы второй ступени, что в 5 - 10 раз выше, чем у второй ступени аэрокосмического самолета типа Sänger. Исключение таких элементов как крыло и вертикальное оперение второй ступени, а также ее простая геометрическая форма, близкая к конусу или оживальному телу [2], позволит создать интегрированную компоновку с частичным утапливанием второй ступени на режиме совместного полета. Это даст возможность существенно приблизить максимальное аэродинамическое качество аэрокосмического самолета при разгоне к величине (L/D)max первой ступени, важность чего будет ясна из дальнейших оценок. |
| Последние разработки, осуществляемые в США, показывают, что возможно создание бескрылого многоразового аэробаллистического аппарата с горизонтальной посадкой, относительная масса конструкции которого близка к величине m(s) носителя Delta Clipper [10]. Соответствующий вариант второй ступени также может быть использован в рассматриваемой концепции. |
| |
II - АЛЬТЕРНАТИВНЫЙ ДВУХСТУПЕНЧАТЫЙ АЭРОКОСМИЧЕСКИЙ САМОЛЕТ |
| Изложенные выше простые и ясные соображения не исчерпывают, однако, рассматриваемую проблему. Встает принципиальный вопрос: насколько в этом случае уменьшится относительная масса полезной нагрузки первой ступени? Для его решения автором была разработана элементарная математическая модель летных данных первой ступени аэрокосмического самолета, описанная в общих чертах в приложениях A и B. |
| Характеристики первой ступени аппарата Sänger были использованы для оценки работоспособности этой математической модели, а также в качестве базовых данных. Первоначально была рассмотрена модель плоского выведения полезных нагрузок на орбиту, причем в этом случае пренебрегалось также длиной участков взлета и снижения. Предполагалось, что аппарат типа Sänger совершает взлет, разгон до M = 4.5, осуществляет крейсерский полет при этом числе Маха, далее он разгоняется до M = 7, затем происходит разделение ступеней и обратный полет при M = 4.5. Траектория альтернативного двухступенчатого аэрокосмического самолета в этом случае была аналогична, за исключением того, что его крейсерский полет происходит при M = 8, разделение ступеней при M = 12.5, а число Маха возвращения в зависимости от варианта изменяется в пределах M = 8 - 10. |
| Зависимость относительной массы топлива первой ступени f1 = mF/m1 (отношения массы израсходованного топлива к ее стартовой массе) от числа Маха полетаM показана для аэрокосмического самолета типа Sänger (m1/m2 = 2.25) на рис. 1 (ломаная линия S). Пунктиром обозначены участки торможения, не требующие в рамках упрощенной модели затрат топлива. Аналогичные характеристики для альтернативного аппарата, использующего известные решения в гиперзвуковой аэродинамике и схемах силовых установок (АКС-1, m1/m2 = 2.25), продемонстрированы на рис. 1 ломаной линией 1. |
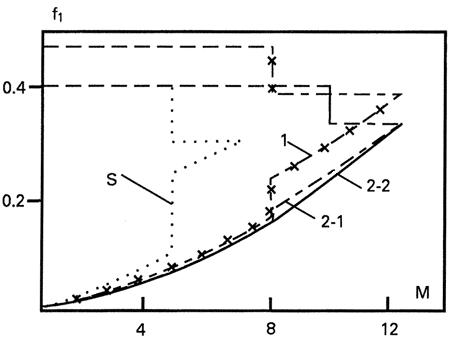 |
| Рис. 1 - Расход топлива в случае плоского выведения |
| При сохранении заданной дальности полета на параллакс R0 = 3000 км необходимая относительная масса топлива первой ступени f1 АКС-1 возросла с 0.40 до 0.47. Это соответствует росту отношения массы топлива, размещаемого на первой ступени аэрокосмического самолета, к массе ее конструкции в 1.35 раза, что является чрезвычайно трудной, а может быть и невыполнимой задачей при создании рассматриваемых двухступенчатых систем в предвидимом будущем. |
| Оценки показывают, что при сохранении радиуса действия и относительной массы топлива первой ступени f1 = 0.40, как у аппарата типа Sänger, стартовая масса первой ступени АКС-1 должна относиться к стартовой массе второй ступени как 6.50 : 1. При этом относительная масса полезной нагрузки АКС-1 составит около 4.5 %, что не слишком превосходит ее максимальные значения для аэрокосмического самолета типа Sänger (2.5 %), и в таком исполнении альтернативная схема многоразового носителя не является чрезмерно привлекательной. Однако, использование уже найденных новых фундаментальных решений в схемах воздушно-реактивных двигателей и, особенно, в гиперзвуковой аэродинамике приводит к кардинальному изменению этой оценки. |
| Важнейшим фактором, определяющим основные характеристики космической транспортной системы при заданной дальности полета для обеспечения необходимого параллакса орбиты полезной нагрузки является максимальное аэродинамическое качество (L/D)max при гиперзвуковых скоростях. Численные исследования в рамках предложенной автором интерференционной концепции аэродинамического проектирования гиперзвуковых летательных аппаратов (некоторые результаты опубликованы в работах [11,12]) позволили проанализировать влияние геометрии и режима обтекания на интерференцию крыла и корпуса при гиперзвуковых скоростях полета и найти способы более эффективного формирования и использования возмущенного за головной ударной волной поля течения путем ограниченных изменений геометрии компоновки и введения небольших дополнительных элементов, что приводит к значительному росту величины максимального аэродинамического качества (L/D)max при гиперзвуковых скоростях полета. |
| Испытания в аэродинамической трубе модели, спроектированной на основании этих принципов, продемонстрировали при М = 7 - 10, числах Рейнольдса (5 - 8)·106 и коэффициенте объема модели τ = ν2/3/W = 0.21, где ν - объем корпуса, а W - площадь крыла конфигурации, что близко к величине коэффициента τ АКС Sänger, уровень (L/D)max = 5.75 - 5.6 (см. кривую 2 на рис. 2). В зависимости от числа Маха это на 15 - 30 % выше, чем у известных компоновок (штриховая область 1 на рис. 2). При M = 7 и 9.8 на кривой 2 нанесены отметки, характеризующие среднеквадратичное отклонение величины (L/D)max по результатам соответственно трех и пяти испытаний. Величины максимального аэродинамического качества этой конфигурации при натурных числах Рейнольдса (Re ≈ 108 по длине аппарата) при M = 7 - 12 составят примерно (L/D)max ≈ 7 (штриховая область 3 на рис. 2). |
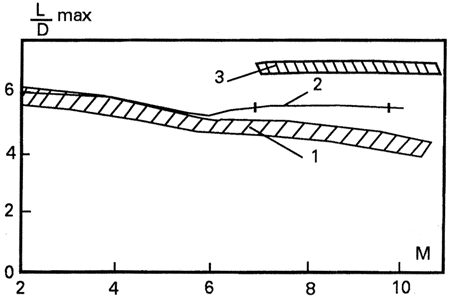 |
| Рис.2 - Уровни максимального аэродинамического качества |
| Оценки показывают, что сбалансированные величины (L/D)max новой компоновки аэрокосмического самолета альтернативной схемы, названного АКС-2, вместе со второй ступенью при натурных числах Рейнольдса будут очень близки к полученным в эксперименте и показанным на рис. 2 кривой 2 значениям максимального аэродинамического качества. При малых и умеренных сверхзвуковых скоростях полета аэродинамические характеристики предлагаемых конфигураций соответствуют характеристикам типичных комбинаций корпуса с крылом малого удлинения. Конструкция разработанных компоновок мало отличается от конструкции классических комбинаций крыла и корпуса. |
| Силовая установка первой крылатой ступени предлагаемого аэрокосмического самолета состоит из прямоточного воздушно-реактивного двигателя, работающего только в режиме сверхзвукового горения (ГПВРД), и воздушно-реактивного двигателя новой схемы, причем оба в качестве топлива используют жидкий водород. Это позволяет существенно упростить конструкцию и улучшить основные характеристики ГПВРД - ключевого элемента эффективного гиперзвукового полета. |
| Двигатель новой схемы, который представляет собой развитие двигателя обратного цикла (I.C.E. ONERA [13,14]), в отличие от существующих в настоящее время и проектируемых силовых установок может работать в непрерывном режиме при числах Маха полета от М = 0 до М = 6 - 7. Предварительные оценки показывают, что на малых скоростях полета его удельные импульс и тяга могут быть близки к соответствующим характеристикам турбореактивного двигателя с форсажной камерой, а с ростом скорости полета вплоть до предельной его характеристики становятся на 15 - 20 % выше, чем у любого известного типа воздушно-реактивного двигателя. |
| В России описываемые конфигурации и схема силовой установки признаны изобретениями, рассматривается возможность их международного патентования. |
| Влияние предлагаемых инноваций приводит к тому, что при m1/m2 = 2.25 относительная масса топлива f1 первой ступени рассматриваемого варианта аэрокосмического самолета АКС-2-1 на модельной траектории плоского выведения полезных нагрузок становится равен 0.40 (рис. 1, ломаная линия 2-1), что совпадает с величиной этого параметра для аппарата типа Sänger |
| Далее был рассмотрен вариант АКС-2-2, аэродинамические характеристики и эффективность силовой установки которого не отличаются от соответствующих параметров АКС-2-1. Однако, если после включения ГПВРД при M ≈ 6.5 участки интенсивного разгона и крейсерского полета заменить на непрерывный этап менее интенсивного и более длительного разгона (ломаная линия 2-2 на рис. 1), то дальность полета АКС-2-2 от старта до достижения точки разделения ступеней при M = 12.5 увеличивается при этом на 10 % по сравнению с дальностью АКС-2-1 при том же расходе топлива. |
| Для анализа основных характеристик первых ступеней аэрокосмических самолетов при пространственном выведении полезных нагрузок на околоземную орбиту необходимо оценить затраты энергии на развороты. Примем во внимание также и расход энергии на кабрирование аэрокосмического самолета перед разделением ступеней. Кроме того, учтем планирование аппарата при возвращении. Основные черты математической модели летных данных первой ступени в этом случае описаны в приложении B. |
| Полученные в соответствии с этой моделью проекции на горизонтальную плоскость траекторий аэрокосмических самолетов типа Sänger и АКС-2-2 в пространственном случае при полете на параллакс показаны на рис. 3 соответственно кривыми S и 2-2. Зависимости относительной массы топлива f1 от числа Маха полета M, а также возможный схематический вид носителей рассматриваемой концепции, представлены на рис. 4. Таким образом, при пространственном выведении полезной нагрузки на орбиту с удалением на юг точки старта второй ступени на расстояние R0 = 3000 км от точки взлета, коэффициент f1 составит для аппарата типа Sänger по проведенным оценочным расчетам величину f1 = 0.38, что на 0.01 меньше, чем величина f1 = 0.39, приводимая при аналогичных условиях его разработчиками, и показанная на рис. 4 точкой PS. Для АКС-2-2 этот параметр равен f1 = 0.39, что только на 0.01 больше, чем для аэрокосмического самолета типа Sänger. Отношение массы топлива первой ступени к стартовой массе всего АКС-2-2составит f0 = 0.27. Если на основе полученных данных математической модели первого приближения оценить поправки второго порядка, тогда величина коэффициента заправочной массы f1 как АКС-2-2, так и аэрокосмического самолета Sänger, необходимая для осуществления описанных выше полетов, составит f1 = 0.39. |
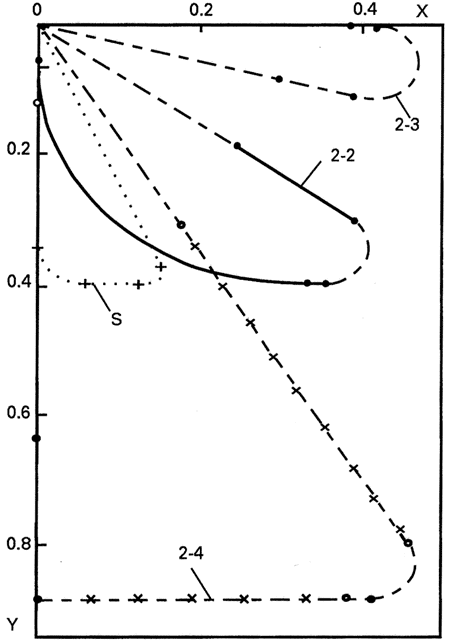 |
| Рис.3 - Проекции траекторий аппаратов |
| Следовательно, расходуемое аппаратом типа Sänger топливо на крейсерский полет с учетом возвращения в точку старта, может использоваться АКС-2-2 на разгон от M = 7 до M = 12.5 и на обратный полет при сохранении радиуса действия и, в первом приближении, доли полезной нагрузки его первой ступени. При этом относительная масса второй ступени не меняется, и указанные выше выигрыши в ее полезной нагрузке приблизительно сохраняются и для всего аэрокосмического самолета в целом. |
| Таким образом, предлагаемая схема двухступенчатого аэрокосмического самолета позволяет, по предварительным оценкам, выводить на низкие околоземные орбиты полезные нагрузки, составляющие 9 - 12 %, и возвращать с орбиты соответственно от 10 % до 0 от его стартовой массы, при радиусе полета на параллакс R0 = 3000 км. Увеличение относительной массы конструкции первой ступени на 10 % по сравнению со ступенью типа Sänger понизит нижнюю границу доли полезной нагрузки до 8 %. |
| Проекция траектории на горизонтальную плоскость и зависимость коэффициента заправочной массы f1 от числа Маха полета M для АКС-2-3, выполняющего полет с нулевым параллаксом, показаны на рис. 3, 4 линиями 2-3. Коэффициент f1 в этом случае будет равен 0.36 (f0 = 0.25), что на 0.03 меньше, чем при полете АКС-2-2 на параллакс, равный 3000 км. |
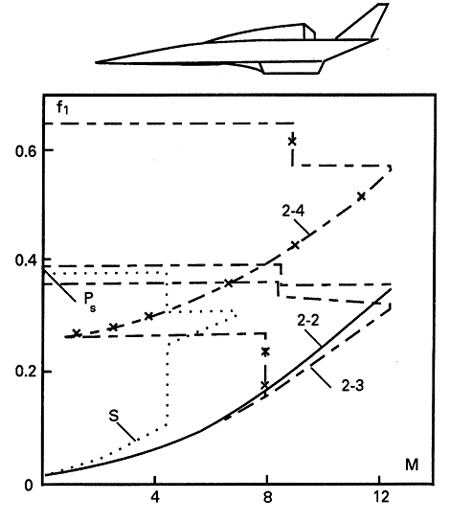 |
| Рис.4 - Расход топлива в случае пространственного выведения |
| Доля топлива в стартовой массе носителя АКС-2-2 с учетом второй ступени составит около 0.44. Если при помощи математической модели из приложений A и B рассмотреть одноступенчатый аналог аппарата, отличающийся от варианта АКС-2-2 только тем, что вместо разделения ступеней и возвращения первой на стартовую позицию, у аналога при M = 12.5 включается водородно-кислородный ракетный двигатель, и аппарат в ракетном режиме выходит на орбиту, то относительная масса топлива возрастет до величины 0.67, то есть не менее, чем в 1.5 раза. Для того, чтобы одноступенчатый аппарат мог выйти на орбиту без полезной нагрузки, относительная масса его конструкции при этом должна уменьшится более, чем в 1.5 раза. Таким образом, для создания одноступенчатого аэрокосмического самолета требуется достижение принципиально более высокого уровня технического совершенства, если это вообще возможно, и в обозримом будущем реален, по-видимому, только двухступенчатый аэрокосмический самолет. |
| |
III - ДОЗАПРАВКА ТОПЛИВОМ В ПОЛЕТЕ |
| Если требуется значительное увеличение радиуса полета первой ступени аэрокосмического самолета с целью расширения диапазона углов наклонения орбит выводимых им полезных нагрузок, то может оказаться необходимым применение дозаправки топливом в полете с дозвукового самолета. Крейсерский полет на достаточно большие расстояния должен совершаться аэрокосмическим самолетом на гиперзвуковой скорости, так как его крейсерские характеристики на дозвуковых скоростях неудовлетворительны, что, в итоге, приводит к уменьшению дальности полета примерно в 2.5 раза. Для дозаправки носитель должен снизить число Маха полета до 0.7 - 0.8, при этом для повторного разгона потребуется значительное количество топлива. Однако, если учесть, что при высоких значениях (L/D)max затраты энергии на разгон в основном преобразуются при планировании в увеличение дальности полета, такая операция становится целесообразной. Возможность дозаправки в полете криогенным топливом требует дальнейших исследований, однако уже более 15 лет назад такая операция рассматривалась в США, как средство увеличения эффективности выведения полезных нагрузок на околоземную орбиту [15,16]. |
| В этом случае полностью заправленный АКС-2-2 может совершить полет на юг на расстояние R0 > 6500 км, после дозаправки осуществить разгон второй ступени до M = 12.5 и вернуться в точку старта (ломаные линии 2-4 на рис. 3 и 4). Выведение полезной нагрузки на экваториальную орбиту становится возможным при широте космодрома не более 60°. Коэффициент заправочной массы при дозаправке составит величину f1 = 0.26 (f0 = 0.18). |
| В заключение следует отметить, что описанные выше идеализированные траектории использовались только для предварительных оценок основных характеристик рассмотренных схем аэрокосмических самолетов. Оптимизация траекторий приведет, в частности, к замене сегментов крейсерского полета и чистого планирования без затрат топлива на некоторый непрерывный участок, с постоянно работающими на нем на малой тяге двигателями. |
| |
IV - ЗАКЛЮЧЕНИЕ |
| Итак, предлагаемая концепция двухступенчатой аэрокосмической транспортной системы Star Liner при умеренном техническом риске позволяет создать аппарат, способный, по предварительным оценкам, выводить на низкую околоземную орбиту полезные нагрузки, составляющие 8 - 12 % от его стартовой массы, что в 5 - 10 раз больше, чем системы Sänger или Delta Clipper, и возвращать на Землю до 10 % от стартовой массы, при радиусе полета около 3000 км. |
| Включение в предлагаемую аэрокосмическую транспортную систему дозвукового самолета-заправщика обеспечит радиус полета первой ступени более 6500 км и позволит снять практически любые ограничения на углы наклонения орбит выводимых этой транспортной системой полезных нагрузок. |
| Более детально исследуемый вопрос был изложен в работе [17]. |
| |
|
Элементарная математическая модель летных данных первой ступени аэрокосмического самолета
при плоском выведении полезных нагрузок на орбиту |
| Как обычно, будем полагать, что на участке взлета расходуется 1 % топлива от стартовой массы аппарата. Кроме того, в модели первого приближения примем величину резерва топлива, равную 2 % от стартовой массы первой ступени аэрокосмического самолета. В дальнейшем все индексы (a) относятся к параметрам разгона, а (c) - крейсерского полета. |
| Известно упрощенное соотношение между относительной массой топлива f, средней по участку траектории величиной отношения тяги к сопротивлению T/D и Δe - отношением приобретенной аппаратом удельной энергии к удельной работе, произведенной силовой установкой аэрокосмического самолета при разгоне [1]: |
| f = 1 - (1 - 0.5Δe/φ)/[1 + Δe(1 + 0.5/φ)] (φ > 0), (1) |
| где f = mF/m, Δe = ΔE/ηQ, E = 0.5V2 + gh, φ = T/D - 1, mF - затраченная на разгон масса топлива, m - стартовая масса, V и h - соответственно скорость и высота на траектории полета, g - ускорение свободного падения, η - средний на участке траектории пропульсивный коэффициент полезного действия двигателей, Q - теплотворная способность топлива (для водорода Q = 1.2·108 Дж/кг). Результаты расчетов по формуле (1) оказались в хорошем согласии с данными летных экспериментов на гиперзвуковом аппарате X-15 (Mmax = 6.5 - 6.7, Δe ≈ 1) [1]. Оценка параметра Δe для любой части траектории разгона рассматриваемых аппаратов показывает, что Δe < 0.1. |
| Для средней по участку траектории величины отношения тяги к сопротивлению T/D = φ + 1 и для среднего значения нормальной перегрузки n, в квазистационарном приближении, пренебрегая проекцией веса на направление касательной к траектории, легко получить соотношение: |
| S = R ln(z)/[n(φ + 1)], (2) |
| где S - длина рассматриваемого участка траектории, R = ηQ(L/D)/g, (L/D) - среднее аэродинамическое качество на нем, z - отношение начальной и конечной масс аппарата на данном участке. |
| Обозначим через ω отношение среднего коэффициента подъемной силы на рассматриваемом участке полета к величине CLc = CLopt = CL((L/D)max), где (L/D)max - максимальное аэродинамическое качество: ω = CL/CLopt. Тогда при квадратичной аппроксимации поляры [12] из выражения (2) следует аналог формулы Бреге для любого пологого участка траектории полета аэрокосмического самолета: |
| S = 2ωRmln(z)/[n(1 + ω2)(φ + 1)], (3) |
| где Rm = ηQ(L/D)max/g. |
| Если подъемная сила L равна весу G, n = 1/ξ, где |
| ξ = (1 - V2/VE2)-1 ≈ (1 - M2/ME2)-1, (4) |
| V - скорость полета, VE - орбитальная скорость, M - число Маха, ME ≈ 25, и при пологом разгоне аппарата мы получаем: |
| Sa = 2ωξRmln(z)/[(1 + ω2)(φ + 1)]. (5) |
| Введем параметр k, характеризующий индивидуальные отклонения различных силовых установок от некоторой типовой кривой η(M), построенной по данным [4,9] (см. [17]). Для аэрокосмического самолета Sänger на крейсерском режиме примем kS = 1. Все длины полета отнесем к некоторой характерной длине S0. Поделив в формуле (3) обе ее части на S0, получим на режиме крейсерского полета аппарата типа Sänger безразмерный параметр σS = (ξSkSηSQ(L/D)S)/(gS0), где индекс (S) обозначает характеристики этого аппарата вместе со второй ступенью на крейсерском режиме, а ξS - определяется из формулы (4) на этом же режиме. Введем параметры p1, p2, p3, p4, p5, где p1 = k/kS, p2 = (L/D)max/(L/D)S, p3 = η/ηS, p4 = ξ/ξS, p5 = 1 для участков крейсерского полета и p5 = 2ω/[(1 + ω2)(φ + 1)] для участков разгона. Тогда выражения (3) и (5) нормируются для любого участка траектории: |
| s = p1p2p3p4p5σSln(z). (6) |
| Анализ аэродинамических характеристик типичных гиперзвуковых компоновок показал, что при скоростных напорах на участках разгона q = 60 - 70 кПа и начальной нагрузке на крыло G0/W = 3 - 3.5 кПа (W - характерная площадь крыла) характерная величина wa = CLa/CLc = 0.5 (ωa ≈ qc/qa). Параметрические исследования среднего отношения тяги к сопротивлению T/D = φ + 1 по формуле (1) привели к выбору для аппарата типа Sänger значений φ = 1.0 (Mmax = 7), а для аэрокосмического самолета альтернативной схемы - φ = 1.5 (Mmax = 12.5). Следовательно, для немецкой концепции на участках разгона p5 = 0.40, для альтернативной - p5 = 0.32. Средние значения параметров p3 и p4 легко вычисляются. Подробности получения оценок параметров p1 и p2 для рассматриваемых аэрокосмических самолетов на различных участках полета приведены в работе [17]. |
| Отношение масс в конце mi+1 и в начале mi каждого участка выражается следующим образом: |
| mi+1/mi = 1/z. (7) |
| Между параметрами z и f существует простая связь: |
| z-1 + f = 1. (8) |
| Из соотношений (1), (6), (7), (8) и |
| s2 + s3 + s4 = s5 = 0.5 (s1 = 0) |
| где si = Si/S0 - безразмерная длина соответствующего участка траектории, итерационным путем можно определить значение безразмерной константы σS = 3.45. |
| Примем, что радиус полета R0 рассматриваемых аэрокосмических самолетов составляет 0.4 от номинальной дистанции полета S0. В работе показано, как при пространственном выведении на орбиту полезных нагрузок построить траектории, удовлетворяющие этому условию. Тогда, при номинальном радиусе полета аэрокосмического самолета Sänger R0 = 3000 км [7], номинальная дистанция полета составит S0 = 7500 км. Отсюда легко получить оценку неизвестного автору максимального аэродинамического качества аэрокосмического самолета Sänger на крейсерском режиме вместе со второй ступенью (KS = 4.6), которое используется в соотношении (6) для расчета летных данных аппаратов альтернативной схемы. |
| После того, как по описанной выше модели первого приближения получена связь между скоростью и дальностью полета, при известной зависимости между скоростью и высотой полета можно учесть влияние проекции веса на направление касательной к траектории и ввести эффективное сопротивление: |
| D* = D(1 + δ), |
| где |
| δ = 2ωθ(L/D)max/[nξ(1 + ω2)], |
| θ - средний угол наклона траектории на рассматриваемом участке. Далее можно повторить всю процедуру расчета, определяя параметр φ следующим образом: |
| φ = T/D* - 1, |
| построив, таким образом, модель второго приближения оценки летных данных первой ступени аэрокосмического самолета. |
| |
|
| Элементарная математическая модель летных данных первой ступени аэрокосмического самолета при пространственном выведении полезных нагрузок на орбиту |
| Для анализа основных характеристик первых ступеней аэрокосмического самолета при пространственном выведении полезных нагрузок на околоземную орбиту необходимо оценить затраты энергии на развороты. Учтем также и затраты энергии на кабрирование аэрокосмического самолета перед разделением ступеней. Используя и далее метод осреднения параметров рассматриваемых процессов и полагая, что радиус кривизны траектории на вираже остается постоянным вследствие изменения крена аппарата, легко получить выражение для оценки длины участка траектории на вираже, являющейся в этом приближении частью окружности: |
| st = ξV2Ψ/[gS0(n2ξ2 - 1)0.5], (9) |
| где st = St/S0 - относительная длина траектории виража, а ψ - угол разворота на вираже. |
| После разделения ступеней целесообразно уменьшить на вираже скорость полета до крейсерской, при этом разворот можно осуществлять с выключенными двигателями за счет накопленной ранее энергии. Пренебрегая изменением высоты полета (потенциальная энергия аэрокосмического самолета при M = 12.5 составляет около 5 % от кинетической), нетрудно вывести приближенное соотношение, связывающее снижение скорости на вираже с углом разворота: |
| Vt1/Vto = 1/exp{nξψ/[(L/D)t(n2ξ2 - 1)0.5]}, (10) |
| где Vt0 и Vt1- соответственно начальная и конечная скорости при развороте с торможением, (L/D)t - среднее аэродинамическое качество, при котором совершается этот разворот. |
| Относительная длина участка траектории sp = Sp/S0, на котором выполняется маневр кабрирования на заданный угол ε, в рамках тех же приближений оценивается следующим образом: |
| sp = ξV2ε/[gS0(nξ - 1)]. (11) |
| Для определения дальности планирования используется приближенное выражение: |
| sg = ξ(L/D)maxΔE/gS0, |
| где sg = Sg/S0 - относительная дальность планирования, в качестве ξ и (L/D)max как и ранее принимаются средние на участке планирования величины, а ΔE - изменение в процессе планирования удельной энергии аппарата. |
| Соотношения (6) (параметр p4 в этом случае должен определяться как p4 = nS/n), (7), (8) вместе с выражениями (9) или (11) позволяют оценить расходы топлива на маневры разворота при пространственном выведении полезной нагрузки и кабрирования для разделения ступеней, а соотношение (10) - число Маха полета при выходе из виража с торможением. |
| Описанные процедуры использовались для оценки необходимого количества топлива, затрачиваемого аэрокосмическим самолетом при полете на заданную дальность. При известных летных характеристиках аппарата и основных параметрах его силовой установки, разбивая траекторию полета на сегменты с малым изменением этих величин, при помощи очень простых средств можно получить значительно более точную и детальную картину рассматриваемого процесса. Следует отметить, что, по предварительным данным, расчеты двух основных вариантов рассмотренных траекторий (варианты S и 2-2 в случае пространственного выведения), проведенные с помощью методов оптимизации, показали хорошее согласование с представленным в работе результатами. |
| |
ССЫЛКИ |
- Jones R., Donaldson C. - From Earth to Orbit in a Single Stage. Aerospace America, 25, no 8, 1987.
- Colucci F. - Launching the Delta Clipper. Space, 7, no 6, 1991.
- Kuczera H., Sacher P., Krammer P. - The German Hypersonic Programme - Status Report 1991. AIIA-91-5001, 1991.
- Kors D. L. - Design Considerations for Combined Air Breathing-Rocket Propulsion Systems. AIAA-90-5216, 1990.
- Weinreich H.-L., Grallert H., Parkinson R., Berry W. - Studies on a Scramjet-Propelled Horizontal Launch and Landing Single-Stage-to-Orbit Launcher. AIAA-93-5053, 1993.
- Koelle D. - Sänger Advanced Space Transportation System - Progress Report 1990. AIAA-90-5200, 1990.
- Hirschel E. - Aerothermodynamics and Propulsion Integration in the Sänger Technology Programme. AIAA-91-5041, 1991.
- Tauber M. E., Menees G. P., Adelman H. G. - Aerothermodynamics of Transatmospheric Vehicles. J. of Aircraft, 24, no 9, 1987.
- Minoda M., Sakata K., Tamaki T., Saitoh T., Yasuda A. - Feasibility Study of Air-Breathing Turbo-Engines for Horizontal Take- Off and Landing Space Plane. AIAA-89-2296, 1989.
- Fulghum D. A. - Skunk Works Design May Cut Launch Costs. Aviation Week & Space Technology, 139, no 7, 1993.
- Лобановский Ю. И. - Максимальное аэродинамическое качество конических комбинаций крыла и корпуса при больших сверхзвуковых скоростях. Известия АН СССР, МЖГ, no 3, 1983.
- Лобановский Ю. И. - Режимы интерференции крыла и корпуса при сверхзвуковых скоростях полета. Ученые записки ЦАГИ, 19, no 6, 1988.
- Ribaud Y. - Inverse Cycle Engine for Hypersonic Air-Breathing Propulsion. ISABE 89 - 7111, 1989.
- Casamayou J.- P. - Le Moteur PRIAM Candidat pour le Vol Hypersonique. Air & Cosmos, no 1434/35, 1993.
- Haefeli R. C., Littler E. G., Hurley J. B., Winter M. G. - Technology Requirements for Advanced Earth-Orbital Transportation Systems. NASA CR-2867, 1977.
- Hepler A. K., Bangsund E. L. - Technology Requirements for Advanced Earth-Orbital Transportation Systems. Volume 1: Executive Summary. NASA CR-2878, 1978.
- Лобановский Ю. И. - Концепция перспективной аэрокосмической транспортной системы. Препринт ЦАГИ, no 95, 1994. //
http://www.synerjetics.ru/
|
| |
| 30.05.1994 Ю. И. Лобановский |
| |
|
| |
|