|
|
 |
| |
Асимптотический метод расчета захвата объекта системой двух небесных тел |
| Ю. И. Лобановский |
| |
Краткое содержание |
| В работе описывается асимптотический метод расчета захвата внешнего объекта, пересекающего систему двух небесных тел, то есть выхода этого объекта на орбиту спутника большего из этих тел без реактивного или аэродинамического торможения, но с возможным использованием малых корректирующих реактивных импульсов. Описываемый метод использован для оценки максимально допустимой скорости полета объекта, еще позволяющей его захват системой Земля-Луна. Показано, что при практически приемлемых ограничениях на минимальное удаление траектории пролета от поверхностей Земли и Луны, пассивный захват (теоретически совсем без корректирующих импульсов) возможен, если гиперболический избыток скорости объекта по сравнению с орбитальной скоростью Земли составляет не более 1.65 км/с. При активном захвате, когда допускается использование направленного вдоль траектории движения корректирующего импульса, максимальная скорость захвата возрастает до 1.75 км/с. |
| Ключевые слова: Захват - Выход на орбиту - Асимптотический метод - Сфера действия - Пертурбационный маневр - Прицельное расстояние - Угол разворота траектории - Максимально допустимая скорость - Варианты захвата |
| |
ТАБЛИЦА СИМВОЛОВ |
- a - расстояние между парой небесных тел
- m - масса меньшего тела
- M - масса большего тела
- ρ - радиус сферы действия меньшего тела по отношению к большему
- E - полная удельная энергия объекта
- R - расстояние от центра небесного тела
- r0 - радиус небесного тела
- G - гравитационный параметр
- v - скорость
- v0 - круговая скорость у поверхности большего небесного тела (первая космическая скорость для большего тела)
- v1 - скорость входа объекта в сферу действия большего тела (гиперболический избыток скорости)
- v2 - скорость входа в сферу действия меньшего тела в системе отсчета, связанной с бoльшим телом
- v3 - скорость выхода из сферы действия меньшего тела в системе отсчета, связанной с бoльшим телом
- v4 - скорость выхода из сферы действия большего тела (гиперболический избыток скорости)
- Δv - разность модулей гиперболических избытков скорости до и после пролета
- vd - скорость объекта при минимальном удалении от центра большего тела
- vD - скорость объекта при максимальном удалении от центра большего тела после захвата
- Δvd - тормозной импульс в перицентре облетной траектории
- u - скорость объекта на входе в сферу действия меньшего тела
- u0 - круговая скорость у поверхности меньшего небесного тела (первая космическая скорость для меньшего тела)
- ud - скорость объекта на минимальном удалении от центра меньшего небесного тела
- umax - скорость объекта у поверхности меньшего небесного тела
- Δu - изменение скорости при облете в системе отсчета, связанной с меньшим телом
- w0 - скорость орбитального движения меньшего тела относительно большего
- φ - угол разворота траектории объекта при облете в системе отсчета, связанной с меньшим телом
- Δφ - угол разворота траектории объекта при облете вследствие орбитального движения меньшего тела
- ψ1 - угол между векторами орбитальной скорости меньшего тела и объекта до облета в системе отсчета, связанной с бoльшим телом
- ψ2 - угол между векторами орбитальной скорости меньшего тела и объекта после облета в системе отсчета, связанной с бoльшим телом
- ψ3 - угол между вектором скорости объекта и направлением на центр большего тела
- Φ1 - угол между векторами орбитальной скорости меньшего тела и скорости объекта до облета в системе отсчета, связанной с меньшим телом
- Φ2 - угол между векторами орбитальной скорости меньшего тела и скорости объекта после облета в системе отсчета, связанной с меньшим телом
- b - прицельная дальность маневра
- d - минимальное удаление траектории объекта от центра небесного тела
- D - максимальное удаление траектории объекта от центра небесного тела после захвата
- ω - угловая скорость орбитального движения
- τ - продолжительность облета
- φ1 = φ ± Δφ
- p = (v0/v3)2
- q = a/r0
- s = 2p/q - 1
|
| |
I - Постановка задачи |
| Изучение возможности захвата внешнего объекта, пересекающего систему двух небесных тел (например, планеты и ее спутника), то есть выхода его на орбиту спутника большего из этих тел без реактивного или аэродинамического торможения, несмотря на кажущуюся теоретическую тривиальность подобного явления, может иметь в перспективе большой практический интерес. Поэтому опишем элементарный асимптотический метод расчета захвата, являющийся первым приближением к решению этой задачи динамики космического полета, и позволяющий получить первичные оценки основных параметров захвата, понять основные закономерности этого процесса, а также дать начальные значения параметров для численных методов его расчета и оптимизации. |
| В соответствии с классическими представлениями, описанными, например, в [1], в математической модели захвата, представляющей собой один из вариантов ограниченной задачи трех тел, используем понятие сферы действия небесного тела. Она представляет собой область пространства, в которой притяжение меньшего из рассматриваемой пары небесных тел доминирует над притяжением большего. Последнее означает, что возмущения, то есть разность гравитационных ускорений в любой точке этой области и в центре большего тела, со стороны меньшего небесного тела превосходят возмущения со стороны большего тела, то есть разность его гравитационных ускорений в этой точке и в центре меньшего из пары тел. В этом случае более адекватным является рассмотрение движения объекта как Кеплерова относительно меньшего небесного тела, на которое накладываются возмущения от большего тела, чем обратное, причем в первом приближении эти возмущения исключаются из рассмотрения. Многочисленные расчеты различных задача динамики в рамках более точных моделей показали, что подобный подход приводит к вполне адекватным результатам, позволяющим, как правило, с точностью до долей процента получить значения основных скоростных и энергетических показателей объекта в системе двух небесных тел в том случае, если движение в основном происходит вдали от границы сферы действия [2]. Очевидно, что в случае захвата последнее условие выполняется. |
| Рассматриваемая область приближенно может быть описана как сфера радиуса ρ, центр которой совпадает с центром меньшего из пары небесного тела, причем |
| ρ = a (m/M)2/5 (1) |
| где a - расстояние между центрами пары тел, m - масса меньшего тела, M - масса большего тела из пары. Например, в паре Солнце - Земля радиус сферы действия Земли относительно Солнца составляет 9.25·105 км при среднем радиусе земной орбиты 1.50·108 км, а в паре Земля - Луна радиус сферы действия Луны относительно Земли - 6.62·104 км при среднем радиусе лунной орбиты 3.84·105 км. Таким образом, отношение радиусов сфер действия к орбитальным расстояниям составляет для Земли и Луны 1/162 и 1/5.8, соответственно. С другой стороны, отношение этих радиусов к собственным средним радиусам небесных тел (6.37·103 км и 1.74·103 км), соответственно, равно 145 и 38. В интеграле энергии (см. также [3]) |
| E = v2/2 − G/R = − G/(2R) (2) |
| где E - полная удельная энергия объекта, v - его скорость, R - расстояние от центра сферы действия, G - гравитационный параметр небесного тела, расположенного в центре сферы действия, погрешность в определении величины его слагаемых при переходе от таких значений радиусов к бесконечным составит, соответственно, 0.7% и 2.6%. Поэтому, при расчете движения объекта внутри сферы действия в первом приближении вполне допустимо полагать, что ее граница лежит на бесконечности. В то же время, при расчете движения объекта вне этой сферы действия (в сфере действия большего тела) ее радиус можно принимать равным 0. Затем полученные внешнее и внутреннее решения должны асимптотически сращиваться. |
| |
II - Основные соотношения |
| Таким образом, постановка рассматриваемой плоской задачи оказывается следующей: в масштабе сферы действия более крупного небесного тела (внешнем масштабе задачи) на бесконечности известна скорость захватываемого объекта относительно этого тела v1 (гиперболический избыток скорости). Выбирая в масштабе сферы действия меньшего небесного тела (внутреннем масштабе задачи) прицельное расстояние (длину нормали, опущенной из центра меньшего тела на продолжение вектора скорости объекта), и угол входа (угол между векторами скорости объекта и орбитальной скоростью меньшего тела), определяем, будет ли захвачен объект с заданными траекторными параметрами. При этом можно вычислить также прицельное расстояние по отношению к большему телу, а угол входа в его сферу действия может быть, в принципе, произвольным вследствие орбитального вращения меньшего тела. Варьирование траекторных параметров позволит определить максимальное значение скорости, при котором объект все еще может быть захвачен. |
| При облете любого небесного тела модуль скорости объекта на границе сферы действия этого тела, то есть, в рамках рассматриваемой асимптотической модели на местной бесконечности, одинаков как до, так и после облета этого тела. В то же время, направление скорости изменяется, и при тесном облете на минимальном расстоянии от поверхности небесного тела или от "верхней кромки" ее атмосферы это изменение может быть значительным. В предельном случае этот разворот вектора скорости дает максимальную величину модуля изменения вектора скорости, равную орбитальной круговой скорости в точке траектории, ближайшей к этому небесному телу [1]. Векторное сложение скоростей на входе и на выходе из сферы действия этого тела с собственной скоростью его движения приводит к изменению не только направления, но и модуля скорости объекта относительно большего тела (см. рис. 1). Подобное изменение скорости называется пертурбационным (гравитационным) маневром. Если в результате маневра гиперболическая относительно большего тела скорость становится эллиптической, и, кроме того, такой, что объект не выходит из его сферы действия, то захват объекта парой тел считается осуществленным. |
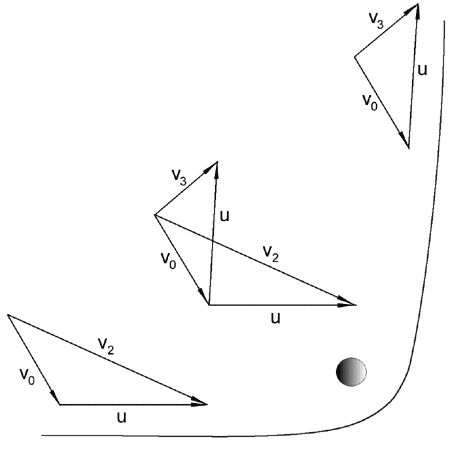 |
| Рис. 1 |
| Обозначим через w0 скорость орбитального движения меньшего тела относительно большего, через v1 - скорость входа объекта в сферу действия большего тела (гиперболический избыток скорости), и через v2 - скорость входа в сферу действия меньшего тела (скорость в точке пересечения траектории с орбитой этого тела). В рамках сделанных асимптотических упрощений из интеграла энергии (2) и определения w0 в случае круговой орбиты |
| w0 = (G/a)1/2 (3) |
| следует, что |
| v2 = (v12 + 2w02)1/2 (4) |
| Складывая скорость объекта относительно большего небесного тела со скоростью орбитального движения меньшего тела, получаем скорость объекта на входе в сферу действия меньшего тела: |
| u = (w02 + v22 ± 2w0v2cosΨ1)1/2, (5) |
| где Ψ1 - угол между векторами его орбитальной скорости w0 и скорости объекта v2, знак перед последним множителем зависит от направления облета. |
| Задавая величину модуля изменения скорости при пертурбационном маневре Δu нетрудно вычислить (см. [1]) угол разворота траектории φ: |
| φ = 2arcsin(Δu/2u), (6) |
| а через него - прицельную дальность маневра b, отнесенную к радиусу небесного тела r0: |
| b/r0 = (u0/u)2/tg(φ/2), (7) |
| где u0 - орбитальная круговая скорость при радиусе r0. Если через d обозначить расстояние до центра небесного тела в точке наиболее тесного сближения с ним объекта, то из закона сохранения момента импульса следует: |
| d/b = u/ud, (8) |
| где ud - скорость объекта в этой точке. Обозначив через umax скорость на расстоянии r0 от центра небесного тела, из (1) получим: |
| umax = (u2 + 2u02)1/2 (9) |
| ud = [umax2 − 2u02(1 − r0/d)]1/2 (10) |
| Из соотношений (8) - (10) достаточно быстро сходящийся итерационный процесс при стартовом значении ud(0) = umax позволяет найти значения d и ud при заданных величинах b и φ. Пока d ≥ r0, такой облет небесного тела возможен. Очевидно, что при тесном облете (d = r0) достигается наибольший разворот вектора скорости объекта, и при определении максимального значения скорости, при котором объект все еще может быть захвачен, должен быть реализован именно такой облет. Если изначально задано прицельное расстояние d, а не величина модуля изменения скорости Δu при пертурбационном маневре, то, используя соотношения (4) - (10) и итерационный процесс типа метода секущих, можно найти все параметры облета. |
| Из рассмотрения треугольника скоростей до облета легко получить, что угол между векторами орбитальной скорости w0 меньшего тела и скорости объекта u в системе отсчета, связанной с меньшим телом, будет равен |
| Φ1 = arcsin[(v2/u)sin(ψ1)] (11) |
| После облета значение этого угла возрастает на величину угла φ. Кроме того, за время движения объекта в сфере действия меньшего тело вследствие его орбитального движения происходит разворот этой сферы действия на дополнительный угол Δφ. При круговой орбите этот угол можно определить как |
| Δφ = ωτ, (12) |
| где ω - угловая скорость орбитального движения, τ - продолжительность облета. Оценить в первом приближении время τ при достаточно тесном облете можно, линейно усредняя скорость движения объекта: |
| τ = 4ρ/(u + ud) (13) |
| Тогда угол Φ2 между векторами орбитальной скорости w0 и скорости объекта u после облета будет равен |
| Φ2 = Φ1 + φ1, (14) |
| φ1 = φ ± Δφ (15) |
| После этого из треугольника скоростей после облета легко определяется модуль скорости выхода из сферы действия меньшего небесного тела в системе отсчета, связанной с бóльшим телом v3: |
| v3 = [w02 + u2 − (± 2w0u cosΦ2)]1/2, (16) |
| угол ее наклона по отношению к орбитальной скорости меньшего тела: |
| ψ2 = arcsin[(u/v3)sin(Φ2)] (17) |
| и при v3 ≥ √2w0 скорость выхода из сферы действия большего тела: |
| v4 = (v32 − 2w02)1/2 (18) |
| Таким образом, разность модулей гиперболических избытков скорости до и после пролета объекта через систему из двух тел составит |
| Δv = v1 − v4 (19) |
| Представляет интерес также угол ψ3 между вектором его скорости и направлением на центр большего тела: |
| ψ3 = ψ2 − π/2 (20) |
| В рамках асимптотической модели захват происходит, если v3 ≤ √2w0, а его границей является условие v3 = √2w0 (v4 = 0). Однако, если учесть конечность сферы действия большего тела, то для захвата надо получить такое значение скорости v3, при котором апоцентр орбиты объекта не находится за его пределами. |
| |
III - Расчет номинального варианта захвата без учета конечных размеров Земли |
| Вернемся теперь к рассмотрению системы Земля - Луна. Считаем в первом приближении, что Луна движется вокруг Земли по круговой орбите. Средняя скорость ее орбитального движения - w0 = 1.02 км/с, угловая скорость - ω = 13.2°/сут, круговая скорость у поверхности Луны u0 = 1.68 км/с. Круговая скорость у поверхности Земли v0 = 7.91 км/с. |
| Известно [1], что максимальный модуль изменения скорости при пертурбационном маневре у Луны Δumax = u0 = 1.68 км/с. Он достигается, когда скорость входа u1 также равна u0, при этом угол разворота траектории φ = 60°. Априори ясно, что при маневре, в котором требуется достичь максимальной разности модулей скорости до и после пролета, значение Δu не должно слишком сильно отличаться от Δumax. Для торможения при облете объект должен догонять Луну (при этом в формулах (5), (16) следует выбирать знак минус), и развернувшись в результате пертурбационного манера против ее движения потерять часть своей скорости относительно Земли. Знак в выражении (15) зависит от того, с какой стороны от Луны проходит объект. При отсутствии дополнительных условий очевидно, что бóльший угол разворота φ1 будет достигнут при облете с внешней по отношению к Земле стороны Луны в направлении ее орбитального движения, причем в формуле (15) в этом случае следует выбирать знак плюс. |
| При линеаризации соотношений (6) - (10) около оптимума по модулю изменения скорости Δu = u0(1 + ε), u = u0(1 + δ1), φ = (π/3)(1 + δ2), b/r0 = √3(1 + δ3), ud = √3u0(1 + δ4), d/r0 = 1 (ε << 1, δi << 1) , легко получить, что |
| ε = o(δi2) (21) |
| Таким образом, в окрестностях этого оптимума при малом изменении других параметров величина Δu изменяется крайне слабо. Далее, нетрудно видеть, что при начальном угле между векторами орбитальной скорости Луны и скорости объекта Φ1 = 60° и угле разворота с максимальным модулем изменения скорости φ = 60° разность v2 - v3 = 2w0cos(φ) = w0 = 1.02 км/с. Если v4 = 0, то v3 = √2w0 = 1.44 км/с, и тогда из выражений (4), (5) и (11) следует, что v2 = 2.36 км/с, ψ1 = 38.1°, а v1 = 1.87 км/с. Таким образом, определяются диапазон скоростей v1 ≥ 1.9 км/с, Δu ≤ 1.68 км/с и углов ψ1 = 35° - 45°, в котором следует искать оптимальное решение асимптотической задачи захвата объекта системой Земля - Луна. |
| Такой численный поиск с использованием выражений (3) - (20) был проделан, и полученный результат, обозначенный как вариант C0 (Capture 0), представлен в верхних строках таблиц 1 - 3. В них параметры (d/r0)1 и (d/r0)2 обозначают отношения минимальных расстояний пролета до центра небесных тел к радиусам, соответственно, Земли и Луны, а параметр Δvd будет описан далее. |
| Легко видеть, что модули скорости объекта в сфере действия Земли при оптимальном захвате близки к предварительным оценкам, однако угол, под которым объект пересекает орбиту Луны, на 6% больше, что позволяет на 5% повысить скорости входа v1 по сравнению с предварительными оценками. При этом скорость u входа в сферу действия Луны увеличивается на 6.5%, а угол разворота траектории гравитационным полем Луну вследствие этого уменьшается на 4.2°. Однако, учет дополнительного фактора - криволинейного движения Луны по орбите вокруг Земли приводит к росту полного угла разворота на 4.3°. Интересно также отметить, что оптимальный облет Луны позволяет уменьшить модуль геоцентрической скорости ровно на 1.00 км/с (от v2 до v3), но нелинейное влияние земной гравитации доводит различие между скоростями входа и выхода на бесконечности почти до 2 км/с (от v1 до 0). |
| При захвате в варианте C0 объект достигает параболической скорости в сфере действия Земли. Однако угол ψ3 между вектором его скорости и направлением на центр Земли мал - ψ3 = 2.2°, что приводит к тому, что этот вариант захвата не может быть использован на практике. Введем параметры: p = (v0/v3)2, q = a/r0 и s = 2p/q - 1. Если p = q/2, то движение объекта происходит по параболической траектории, и из законов сохранения энергии и момента импульса легко получить минимальное удаление траектории объекта от центра Земли: |
| d = r0[q sin(ψ3)]2/(2p) (22) |
| Если p > q/2, то движение объекта происходит по эллиптической траектории, и |
| d = r0{p ± [p2 − sq2sin2(ψ3)]1/2}/s, (23) |
| причем знак минус в формуле (23) соответствует перицентру, а плюс - апоцентру орбиты. При тесных пролетах около Земли более простое и наглядное выражение (22) по существу является первым приближением к решению (23). Поэтому его целесообразно использовать для качественного анализа результатов. Скорость объекта в точке максимального сближения: |
| vd = (a/d)v3|sin(ψ3)| (24) |
| В варианте захвата C0 d < r0, и объект, вместо выхода на орбиту спутника Земли, соударяется с ее поверхностью. Из (22) видно, что для осуществления реального захвата необходимо увеличить модуль угла ψ3, направляя объект в сторону от центра Земли. Анализируя выражения (3) - (20) легко сделать вывод, что для это надо либо увеличивать, либо уменьшать угол ψ1, отклоняя траекторию объекта от оптимизированной без учета этого фактора. |
| |
IV - Варианты выхода на околоземную орбиту |
| При увеличении угла ψ1 одновременно надо снижать скорость v1 входа объекта в сферу действия Земли, иначе либо объект врежется в Луну, либо угол разворота его траектории уменьшится, приводя к потере захвата даже без учета конечности радиуса сферы действия Земли. Предельный случай захвата при увеличенном угле пересечения орбиты Луны и траектории объекта, когда последняя касается как поверхности Луны, так и поверхности Земли ((d/r0)1 = 1.00 и (d/r0)2 = 1.00), обозначен как CAI-1 (Capture-Active-Inverse-1) (см. таблицы 1 - 3). Скорость входа в сферу действия Земли v1 при этом уменьшилась до 1.80 км/с, скорость выхода из сферы действия Луны стала эллиптической (v3 = 1.22 км/с), но итерационный процесс, построенный на соотношениях (25) - (26) |
| D/d = vd/vD (25) |
| vD = [vd2 - 2v02(r0/d - r0/D)]1/2, (26) |
| где D и vD - соответственно расстояние от центра Земли и скорость объекта в апогее, показывает, что апогей полученной в варианте захвата CAI-1 орбиты (D/r0 = 216) примерно в 1.5 раза превышает радиус сферы действия Земли. Однако тормозной импульс Δvd, уменьшающий скорость объекта в перигее всего на 13 м/с, переводит его на орбиту, целиком лежащую в сфере действия Земли. Такой захват, требующий малого корректирующего тормозного импульса в перигее, назовем активным, в противовес пассивному захвату, при котором дополнительные импульсы не требуются. В результате, объект оказывается захвачен Землей, но при этом направление его вращения по эллиптической орбите оказывается противоположным направлению вращения Луны и Земли. |
| При уменьшении угла ψ1 между векторами орбитальной скорости меньшего тела и объекта, одновременно надо снижать скорость v1 входа объекта в сферу действия Земли еще в большей степени, чем при его увеличении, а также увеличивать прицельное расстояние по отношению к Луне для того, чтобы увеличение угла разворота траектории объекта φ не компенсировало уменьшение угла ψ1. Предельный случай захвата при уменьшенном угле пересечения орбиты Луны и траектории объекта, когда последняя касается поверхности Земли ((d/r0)1 = 1.39, (d/r0)2 = 1.00), обозначен как CAD-1 (Capture-Active-Direct-1) (см. таблицы 1 - 3). Скорость входа в сферу действия Земли v1 при этом уменьшилась до 1.71 км/с, а корректирующий тормозной импульс в перигее для того, чтобы апогей оставался в сфере действия Земли, составляет 19 м/с. В этом случае направление его вращения по эллиптической орбите совпадает с направлением вращения Луны и Земли. |
| Варианты захвата CAI-1 и CAD-1 являются оценками теоретических границ активного захвата объекта с выходом на эллиптические орбиты обратного и прямого вращения, когда траектория полета касается поверхности по крайней мере одного из небесных тел. Однако, на практике расстояние в перицентре траектории объекта должно быть больше их радиусов. На мой взгляд, практически приемлемым минимальным расстоянием пролета может считаться величина, составляющая 5% от радиуса небесного тела. Для Луны эта величина равна 70 км, а для Земли - 320 км. Таким образом между условной верхней кромкой земной атмосферы и перигеем траектории будет около 200 км. Аналоги вариантов захвата CAI-1 и CAD-1, но с ограничением (d/r0)i ≥ 1.05, i = 1, 2, названы CAI-2 и CAD-2 соответственно. Для пролета с обратным вращением ужесточение ограничений, накладываемых на траекторию захвата, приводит к снижению скорости входа в сферу действия Земли v1 до 1.75 км/с. В случае прямого вращения величина v1 практически не изменяется. Почти не изменились и перигейные тормозные импульсы (см. таблицу 2). |
| Дальнейшее снижение скорости входа в сферу действия Земли приводит, наконец, к пассивному захвату объекта системой Земля-Луна. Асимптотическая оценка скорости входа на теоретической границе пассивного захвата (при касании поверхности Луны при пролете) составляет 1.69 км/с при обратном вращении объекта (вариант CPI-1 (Capture-Passive-Inverse-1)), и 1.51 км/с при прямом (вариант CPD-1 (Capture-Passive-Direct-1), см. таблицу 2). При всех вариантах пассивного захвата скорость выхода из сферы действия Луны v3 составляет 1.11 км/с, что на 0.33 км/с меньше, чем параболическая скорость на лунной орбите. Следует также отметить, что даже на теоретической границе при пассивных захватах с обратным вращением перигей орбиты объекта более чем в 3 раза превышает земной радиус. Переход к оценкам практической границы захвата (варианты CPI2 и CPD2) приводит к небольшому снижению скорости входа v1 до 1.67 км/с и 1.50 км/с для орбит обратного и прямого вращения соответственно (см. таблицу 2). После захвата можно использовать пролеты объекта мимо Луны и/или корректирующие реактивные импульсы для формирования его окончательной парковочной орбиты. |
| |
V - Заключение |
| Таким образом, асимптотический метод расчета захвата позволяет оценить скорость входа в сферу действия Земли, при которой еще возможен активный захват объекта, значениями около 1.70 км/с и 1.75 км/с в зависимости от направления его вращения на орбите захвата, и, соответственно, около 1.50 км/с и 1.65 км/с при пассивном захвате. При обратном вращении максимальные скорости захвата выше на 0.05 - 0.15 км/с. |
| |
| Таблица 1 |
| Обозначения | Расшифровка обозначений |
| C0 | Номинальный захват |
| CAI | Активный захват с обратным вращением |
| CAD | Активный захват с прямым вращением |
| CPI | Пассивный захват с обратным вращением |
| CPD | Пассивный захват с прямым вращением |
| 1 | Теоретический вариант |
| 2 | Практический вариант |
|
| |
| Таблица 2 |
| Характерные скорости и расстояния при захвате |
| Вариант | v1 (км/с) | v2 (км/с) | u (км/с) | Δu (км/с) | (d/r0)1 | v3 (км/с) | (d/r0)2 | Δvd (м/с) |
| C0 | 1.97 | 2.44 | 1.79 | 1.68 | 1.00 | 1.44 | - | - |
| CAI-1 | 1.80 | 2.30 | 1.71 | 1.68 | 1.00 | 1.22 | 1.00 | 13 |
| CAD-1 | 1.71 | 2.24 | 1.52 | 1.42 | 1.39 | 1.28 | 1.00 | 19 |
| CAI-2 | 1.75 | 2.27 | 1.69 | 1.64 | 1.05 | 1.20 | 1.05 | 12 |
| CAD-2 | 1.71 | 2.24 | 1.52 | 1.42 | 1.40 | 1.28 | 1.05 | 19 |
| CPI-1 | 1.69 | 2.22 | 1.71 | 1.68 | 1.00 | 1.11 | 3.02 | 0 |
| CPD-1 | 1.51 | 2.08 | 1.38 | 1.29 | 1.69 | 1.11 | 1.00 | 0 |
| CPI-2 | 1.67 | 2.20 | 1.69 | 1.64 | 1.05 | 1.11 | 2.54 | 0 |
| CPD-2 | 1.50 | 2.08 | 1.37 | 1.29 | 1.70 | 1.11 | 1.05 | 0 |
|
| |
| Таблица 3 |
| Характерные углы при захвате |
| Вариант | ψ1° | Φ1° | φ° | Δφ° | φ1° | Φ2° | ψ2° | ψ3° |
| C0 | 40.5 | 62.2 | 55.8 | 8.5 | 64.3 | 126.5 | 92.2 | 2.2 |
| CAI-1 | 43.1 | 67.2 | 59.0 | 8.7 | 67.7 | 134.9 | 98.7 | 8.7 |
| CAD-1 | 34.9 | 57.4 | 55.9 | 10.0 | 65.9 | 123.3 | 81.7 | − 8.3 |
| CAI-2 | 44.0 | 68.8 | 58.0 | 8.8 | 66.8 | 135.7 | 99.1 | 9.1 |
| CAD-2 | 34.8 | 57.3 | 55.9 | 10.0 | 65.9 | 123.2 | 81.5 | − 8.5 |
| CPI-1 | 47.6 | 73.8 | 59.0 | 8.7 | 67.7 | 141.5 | 106.7 | 16.7 |
| CPD-1 | 35.1 | 60.6 | 55.9 | 11.0 | 66.9 | 127.4 | 80.4 | − 9.6 |
| CPI-2 | 47.5 | 73.9 | 58.0 | 8.8 | 66.8 | 140.8 | 105.3 | 15.3 |
| CPD-2 | 35.1 | 60.3 | 55.9 | 11.0 | 66.9 | 127.2 | 80.2 | − 9.8 |
|
| |
ССЫЛКИ |
- Левантовский В. И. - Механика космического полета в элементарном изложении. Москва, Наука, 1980.
- Ильин В. А., Кузмак Г. Е. - Оптимальные перелеты космических аппаратов с двигателями большой тяги. Москва, Наука, 1976.
- Левин К. Е., Лобановский Ю. И. - О гравитационных потерях при полетах с малой тягой, 2003 //
http://synerjetics.ru/
|
| |
| 12.12.2003 Ю. И. Лобановский |
| |
|
| |
|