SYNERJETICS GROUP Рассматривается инцидент с «танцующим» Волгоградским мостом. Показано, что причиной волнообразных движений верхнего строения моста явился вход в начало срывного флаттера, то есть в автоколебания системы, состоящей из потока сплошной среды и твердого тела, вызываемые сходящими с тела вихрями Кармана.

Главная страница

Эволюция сложных систем

О пределах развития

Несистемность

Классификатор проблем

Изменение сценария

Пассионарные толчки

Флаттер мостов

Катастрофа на СШ ГЭС

Падение температуры Земли

Презентации

Пионеры космонавтики

Классификация проблем

Последствия мощных импактов

Функциональная архитектура

Complex Systems Evolution

Temperature Drop

Обратная связь

Дело о «танцующем» мосте

Ю.И.Лобановский

А дело, которое привело нас сюда, быстро приближается к развязке.

А. Конан Дойл, «Пляшущие человечки».

Краткое содержание

В работе рассматривается инцидент с «танцующим» Волгоградским мостом. Показано, что причиной волнообразных движений верхнего строения моста явился вход в начало срывного флаттера, то есть в автоколебания системы, состоящей из потока сплошной среды и твердого тела, вызываемые сходящими с тела вихрями Кармана. Предложена интерполяционная формула оценки числа Струхаля для срывного обтекания тел с плоскими гранями. Проведена оценка частот вихревых колебаний для висячего Такомского и балочного Волгоградского мостов, вызванных их ветровым обдувом. Описаны произошедшие ранее инциденты с ветровыми колебаниями балочных мостов, по крайней мере, один из которых завершился разрушением моста. На основе теории гидроакустического возбуждения автоколебаний напорных систем был разработан аналогичный подход для оценки аэроупругой устойчивости мостов. Предложен комплекс работ, которые следует провести для подтверждения предлагаемого подхода, а также для полного устранения ветровых колебаний рассматриваемых балочных мостов.

Ключевые слова: Волгоградский мост – «танцующий» мост – Такомский мост – инцидент – срывной флаттер – вихри – дорожка Кармана – автоколебания – устойчивость – аэроупругий резонанс – гидроакустический резонанс – собственная частота колебаний – вихревая частота – критерий возбуждения – гасители колебаний

ТАБЛИЦА СИМВОЛОВ

b - продольный (по потоку) размер сечения тела
d - поперечный размер сечения тела
λ = b/d - удлинение тела
L - продольное расстояние между вихрями в дорожке Кармана
h - поперечное расстояние между вихрями в дорожке Кармана
v - скорость потока (ветра)
u - скорость движения вихрей
Γ - циркуляция
ρ - плотность
μ - коэффициент динамической вязкости
ν - частота
θ - добротность колебательной системы
β - логарифмический декремент
γ - показатель степени
Re - число Рейнольдса
St - число Струхаля
St₀ - число Струхаля плоской пластинки по Карману
σ - индекс устойчивости
m - кратность частот
k_σ - нормировочный множитель
z - зональный коэффициент
k_s - коэффициент состояния системы
q - интерполяционный коэффициент

Индексы нижние:

e - собственный
p - возбуждающий
v - вихревой

Индексы верхние:

* - критический

I – Введение

20 мая 2010 года в 18:40 по московскому времени было перекрыто автомобильное движение по новому мосту через реку Волгу в городе Волгограде, так как начались колебания пролетов моста, размах которых достиг почти одного метра [1, 2]. Все это продолжалось около часа. Волгоградский мост, существующий в настоящее время – это объект, полученный в результате завершения первой очереди строительства: поставлены все опоры, попарно расположенные рядом друг с другом, и уложена половина верхнего строения. Первая очередь моста была открыта 10 октября 2009 года, то есть за 7 с небольшим месяцев до инцидента [1].

Первоначально инцидент не привлек серьезного внимания автора этой работы вследствие того, что причина колебаний моста была достаточно очевидна с первого взгляда. Однако, несколько дней спустя к нему обратились за консультациями по этому инциденту, и ему пришлось в нем разбираться. Как известно, «аппетит приходит во время еды», и в согласии с этим психологическим феноменом данный случай также постепенно показался достаточно интересным для дальнейшей более углубленной работы. Кроме того, при рассмотрении этого явления с общих позиций теории колебаний, оно оказалось очень близким к тому, что занимало автора последние несколько месяцев – гидроакустическому возбуждению автоколебаний в напорных системах гидроэлектростанций. Те явления не менее чем трижды приводили к частичному или полному разрушению гидроагрегатов, а в одном инциденте на Саяно-Шушенской ГЭС – и к разрушению машинного зала практически со всеми агрегатами [3, 4], и возможность увязать эти события с другими потенциально опасными явлениями показалась небезынтересной. Вследствие этих обстоятельств и появилась данная работа, повествующая о результатах короткого расследования этого достаточно простого дела.

II – Параметры Волгоградского моста и характеристики инцидента

Волгоградский мост общей длиной около 1260 м [1] представляет собой балочную конструкцию не менее чем из 12 пролетов, 9 из которых хотя бы частично находятся в створе реки (см. рис. 1) [5]. Длина каждого из них превышает 100 м или близка к этой величине. Верхнее строение моста – металлическое, на опорах находится ортотропная плита, состоящая из плоских стальных листов и объединенных с ними ребер жесткости облегченной конструкции с толщиной стенок 10 – 12 мм [6]. Ширина асфальтобетонного полотна, уложенного на верхнее строение, после завершения первой очереди строительства составляет 16 м, то есть половину от проектной.

Для определения длины основных пролетов Волгоградского моста и ширины дорожного полотна были использованы фотоснимки спутников дистанционного зондирования Земли [5]. Ранее сравнением по таким изображениям длины 11 различных объектов с их истинными значениями было показано, что в диапазоне длин 300 – 5500 м среднеквадратичное отклонение составляет не более 0.55 %, а в диапазоне длин 300 – 1000 м (4 объекта) – не более 0.75 %. Из спутниковых фотографий следует, что длины основных пролетов моста, начиная с правого берега реки (находящегося на снимке слева), составляют последовательно 130 м, 3 по 155 м, 3 по 126 м и затем – 2 по 86 м (см. рис. 1), а точность их определения составляет порядка 1 м.

Рис. 1

Из сопоставления кадров видеофильма [7], снятого во время инцидента (см. рис. 2 – 4), и спутниковой фотографии (рис. 1), следует также, что колебалось верхнее строение моста, расположенное, в основном, на его пролетах длиной 155 м. Частота колебаний была порядка ν ~ 0.5 Гц. Колебания были практически чисто изгибными, признаков заметного кручения полотна моста не зафиксировано (см. рис. 4). Источник [8] также сообщает, что колебания происходили «в судоходных пролетах моста длиной 155 м». Известно, что колебания происходили при ветре, дующем вдоль реки со скоростью 15 – 17 м/с [9].

Рис. 2

Рис. 3

Рис. 4

Любой человек, имеющий отношение к мостам или к аэроупругости, в описываемой ситуации тут же вспоминает о Такомском мосте (Galloping Gertie), который 7 ноября 1940 при ветре, дувшем вдоль пролива Такома-Нэрроуз со скоростью 17 – 19 м/с, более часа совершал сначала изгибные колебания из-за срывного флаттера (см. рис. 5), а, затем, после обрыва части подвесок, за полчаса изгибно-крутильных колебаний большой амплитуды разрушился [10 – 13]. При этом он был правильно рассчитан на статические нагрузки, возникающие при ветре до скорости 45 м/с [13]. Как известно, та авария способствовала исследованиям в области аэродинамики и аэроупругости конструкций и изменению подходов к проектированию всех большепролетных мостов в мире. Однако, все это относилось только к подвесным или вантовым мостам, а не к балочным, каковым является Волгоградский мост. Тем временем, совершенствование способов проектирования постепенно привело к тому, что и балочные мосты стали значительно более тонкими, легкими, изящными и, соответственно, менее жесткими, чем ранее [6]. Несмотря на это в нормативных документах, которыми конструкторы руководствуются при проектировании балочных мостов, это не было отражено, и их аэроупругие характеристики доселе не рассматриваются вовсе [6, 14, 15].

Рис. 5

Да и с вантовыми мостами, как показывает опыт, сейчас далеко не все в порядке. Не далее как с полмесяца назад, 11 июня 2010 года были замечены значительные колебания основного пролета Живописного моста в Москве, открытого в конце декабря 2007 года [16, 17]. Очень сильно колеблется и мост через Оку в Муроме, и, якобы, уже недалеко до его закрытия, а ведь он был введен в эксплуатацию 1 октября 2009 года [18, 19].

Считается, что волгоградский инцидент – первый случай, когда ветровая нагрузка привела к сильным колебаниям балочного моста [6]. Можно отметить, что такое же мнение до сих пор, по-видимому, бытует и об инциденте с отрывом турбинной крышки и взлетом второго гидроагрегата Саяно-Шушенской ГЭС, как о первом в истории. Но в обоих случаях общепринятые мнения, как это часто бывает, являются ошибочными. Беспомощность объяснений этих явлений некоторыми специалистами (например, попытки объяснить колебания Волгоградского моста в течение, примерно, часа согласованными с ними пульсациями ветра [8]) стала для автора этой работы уже привычной обыденностью. А постоянное стремление представителей официальных властей интерпретировать все такие инциденты как «сверхъестественные явления» [9], то есть явления, не подчиняющиеся законам природы, можно по теории З. Фрейда объяснить просто необходимостью подавить в себе страх перед любыми законами, как человеческими, так и божьими.

III – Известные виды флаттера – автоколебаний твердых тел в потоке жидкости или газа

Так что же такое флаттер, из-за которого не только разрушился Такомский мост, но в тот же период времени в одной Германии с 1935 по 1943 год разбилось около 150 самолетов [12]? Флаттер – это автоколебания твердого тела или системы механически связанных между собой твердых тел в потоке сплошной среды, то есть жидкости или газа, вместе с этой средой. Этим флаттер отличается от других видов автоколебаний, происходящих в сплошных средах, при которых твердые тела остаются неподвижными, по крайней мере, на начальной стадии и в теоретических моделях этих процессов. Как у любого автоколебательного процесса, у флаттера должен иметься механизм положительной обратной связи, который обеспечивает перекачку энергии к нему из окружающей среды. По типу этого механизма можно выделить изгибно-крутильный флаттер, «многозвенный» (в авиации наиболее типичный его вариант называют изгибно-элеронным) [20] и срывной флаттер.

В изгибно-крутильном флаттере положительная обратная связь реализуется, если линия центров инерции тела находится по потоку за линией центров жесткости, что при отсутствии специальных мер является типичной ситуацией для таких тел, как, например, крыло самолета. Тогда при изгибных колебаниях крыла оно закручивается так, что дополнительная аэродинамическая сила на нем, вызванная кручением, действует в ту же сторону, куда крыло движется во время своего маха, усиливая его. Таким образом, эти изгибные махи экспоненциально растут, усиливая сами себя, пока крыло не разрушится [20].

В «многозвенном» флаттере принимает участие система не менее чем из двух механически связанных твердых тел, на практике обычно крыла и элерона – отдельной небольшой аэродинамической поверхности, расположенной за основным крылом. При этом в отличие от бафтинга между телами рассматриваемой колебательной системы нет заметных пространственных промежутков (элерон, в отличие, скажем, от хвостового оперения, располагается непосредственно на крыле). В таком случае кручение крыла уже не обязательно, а источником положительной обратной связи является этот самый элерон, движущийся относительно крыла так, что создает дополнительную аэродинамическую силу системы крыло-элерон в направлении маха крыла [20]. В остальном механизм положительной обратной связи такой же, как и в предыдущем типе флаттера. Оба этих типа флаттера возникают на хорошо обтекаемых телах, когда в базовую математическую модель явления нет необходимости включать вязкость сплошной среды, а решение ищется для невязкого потенциального потока (потенциального везде, за исключением особых точек, число которых равно числу тел колебательной системы).

В отличие от кратко описанных выше типов флаттера, для появления и развития срывного флаттера, возникающего на плохообтекаемых телах, вязкость потока имеет принципиальное значение. Именно вследствие действия вязкости в потоке за такими телами возникают периодические структуры вихрей, называемые дорожками Кармана в честь выдающегося аэродинамика XX века Теодора фон Кармана, построившего первую адекватную математическую модель этого явления 98 лет назад. Сами дорожки Кармана с помощью простых методов визуализации, а иногда, даже и без них, можно наблюдать практически за любой преградой, возникающей на пути потока, как воздуха, так и воды (см., например, на рис. 6 фотографию 94 из источника [21], полученную при обтекании водой кругового цилиндра).

Рис. 6

Механизм положительной обратной связи при автоколебаниях тел, создающих такие дорожки, обеспечивается тем, что колебания тела усиливают вихреобразование, которое в свою очередь увеличивает силы и моменты, действующие на тело, и, следовательно, его колебания [22]. В отличие от изгибно-крутильного флаттера механизм перекрестного взаимодействия прямолинейного и крутильного движений элементов тела здесь не играет существенной роли, поэтому срывной флаттер может быть практически чисто изгибным (см. рис. 7, схематически изображающий дорожку Кармана в окрестности тела, моделирующего верхнее строение моста).

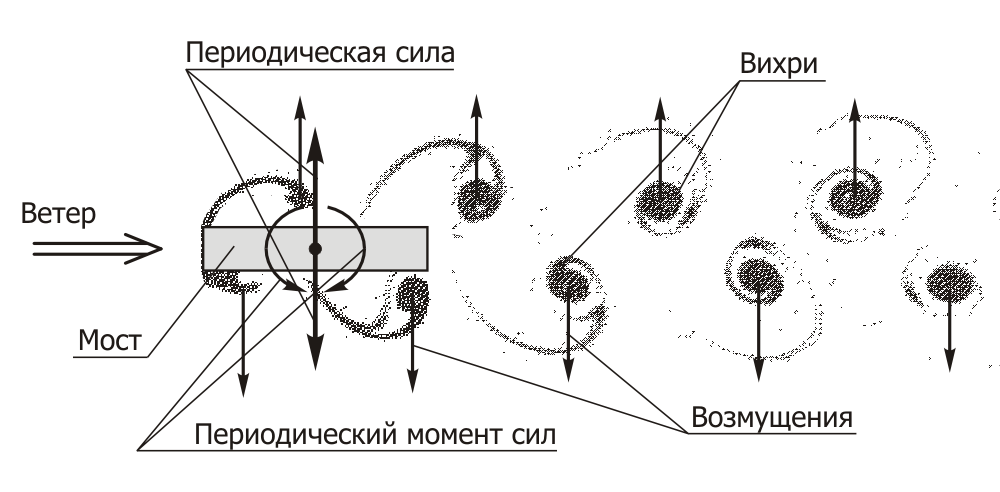Рис. 7

При срывном флаттере на тело кроме подъемной силы, перпендикулярной направлению набегающего потока действует также и сила лобового аэродинамического сопротивления, направленная по потоку. Кроме постоянной компоненты сила сопротивления также имеет и колебательную вихревую компоненту, частота которой вдвое выше частоты вихревой подъемной силы. Разница частот возникает из-за того, что частота подъемной силы определяется расстоянием между вихрями только вдоль одной из сторон дорожки Кармана, а частота периодической компоненты лобовой силы определяется расстоянием между вихрями вдоль обеих ее сторон [22]. Переменная компонента лобовой силы обычно мала по сравнению с подъемной силой и, поэтому, на рис. 7 для простоты не показана.

IV – Основные закономерности срывного флаттера

Для наших целей нет необходимости подробно разбираться во всех тонкостях срывного флаттера, а достаточно использовать основные результаты теории этого явления. Частота появления вихрей ν_v при таком флаттере, которая является частотой возбуждения ν_p автоколебаний системы, вычисляется следующим образом:

(1)

где St – число Струхаля (безразмерный параметр подобия), v – скорость потока, d – поперечный размер плохо обтекаемого тела. По существу формула (1) и является определением числа Струхаля, и поэтому, казалось бы, она не может являться рабочим инструментом для каких-либо вычислений.

Однако, имеется замечательное свойство таких срывных течений, заключающееся в том, что в очень широком и практически интересном диапазоне определяющих процесс параметров число Струхаля при заданной форме тела остается почти постоянным. Кроме того, даже там, где это число не постоянно, оно зависит только от единственной безразмерной их комбинации – параметра подобия, называемого числом Рейнольдса Re:

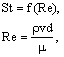
где ρ – плотность сплошной среды, μ – коэффициент ее динамической вязкости. На рис. 8, заимствованном из источника [23], показана зависимость числа Струхаля St от числа Рейнольдса Re при изменении последнего от 3·10¹ до 3·10⁵ при обтекании кругового цилиндра, расположенного поперек потока.

Рис. 8

Из графика видно, что при числах Рейнольдса от 3·10² < Re < 3·10⁵ число Струхаля St = 0.20 ± 0.02. При скорости ветра 10 – 20 м/с и температуре воздуха около 290 К эти значения параметра подобия соответствуют диаметру цилиндра от 0.2 мм до 0.5 м (см. [24, 25]), что охватывает весь диапазон размеров от проволочек измерительных приборов и струн «эоловой арфы» до самых толстых вант подвесных мостов. При числах Рейнольдса 5·10⁵ < Re < 5·10⁶ дорожка вихрей за круговым цилиндром становится сильно турбулентной, так что число Струхаля становится невозможно определить. Далее, при Re > 5·10⁶ число Струхаля снова стабилизируется и оказывается равным St ≈ 0.3 [22]. Все это относится к частоте возбуждения колебаний, направленных перпендикулярно скорости потока, то есть частоте подъемной силы вихрей. Если необходимо рассчитать обычно многократно более слабые колебания вдоль вектора скорости потока, то в числитель формулы (1) следует ввести множитель 2.

Есть еще одно свойство числа Струхаля при срывном флаттере, которое, может быть, даже еще более полезно для решения поставленной задачи – вычисления частоты возбуждения колебаний при ветровом обдуве мостов. Это его свойство заключается в том, что число Струхаля достаточно слабо зависит также и от формы поперечного сечения тела, особенно если на поверхности тела имеются ребра, фиксирующие положение отрывов, порождающих вихри. Из классического решения Кармана, выведенного для потока невязкого везде, за исключением двух точек на теле, и получаемого предельным переходом по числу Рейнольдса, следует, что для кругового цилиндра число Струхаля St ≈ 0.20 [26]. Из графика на рис. 8 следует, что эта величина хорошо согласуется с экспериментальными данными при 3·10² < Re < 3·10⁵. Кроме цилиндра Карманом было рассмотрено обтекание еще одного тела – плоской пластинки, поставленной поперек потока [26]. Для нее обработка результатов расчетов и экспериментов привела к значению числа Струхаля St ≈ 0.145. Если поперечное сечение тела является квадратом, то число Струхаля для него будет практически такое же, как для пластинки – St ≈ 0.14 [27].

Единственным качественным отличием рассматриваемых зависимостей St = f(Re) для пластинки или тела с поперечным сечением типа прямоугольника, которое сразу можно предсказать, является то, что критическая величина числа Рейнольдса, при котором начинается сильно турбулентная зона, где число Струхаля невозможно определить, будет значительно больше, чем для кругового цилиндра, если эта граница для них существует вообще. Этот прогноз вызван тем, что при критической величине числа Рейнольдса Re* ≈ (1.5 – 3)·10⁵, в случае обтекания трехмерного тела, в поперечном сечении совпадающим с круговым цилиндром, возникает явление, имеющее прямое отношения к рассматриваемым срывным течениям. Данное явление называется кризисом обтекания шара [28]. Оно обычно описывается как резкое падение аэродинамического сопротивления шара и вызвано быстрым, но неустойчивым стягиванием точек схода вихрей из периферийных районов поверхности шара ближе к его оси, параллельной набегающему потоку, вследствие перемещения точек отрыва пограничного слоя. При этом натурным условиям с относительно малой начальной турбулентностью потока соответствует верхняя граница критических величин числа Рейнольдса Re* ≈ 3·10⁵.

Аналогичный кризис обтекания при несколько бóльших критических числах Рейнольдса возникает и при обтекании кругового цилиндра. Из этого можно сделать вывод, что именно кризис обтекания приводит к сильной турбулизации дорожки вихрей Кармана за цилиндром при Re* ≈ 5·10⁵. В новой конфигурации вихрей дорожка теряет устойчивость, и при Re ≥ 5·10⁵ вместо нее образуется так называемый турбулентный спутный след. Как уже упоминалось, в отличие от тел с гладкими поверхностями на телах с разрывами гладкости поверхности (ребрами) вихри вне зависимости от значений числа Рейнольдса всегда сходят с этих ребер. Поэтому как для пластины, так и для тела, сечение которого изображено на рис. 7, точки схода вихрей всегда сохраняют свое неизменное положение, и зона определенных и устойчивых значений числа Струхаля вследствие этого должна быть распространена до значительно бóльших чисел Рейнольдса, возможно, вплоть до перекрытия со следующей зоной устойчивости, начинающейся где-то в окрестности Re ~ 10⁷.

Из условия устойчивости дорожки вихрей, полученного в теории Кармана, следует, что существует единственное фиксированное отношение между поперечным h и продольным расстояниями L между вихрями [26]:

(2)

откуда

Для шахматного расположения цепочек, когда каждый вихрь верхней цепочки располагается точно посередине между ближайшими вихрями нижней цепочки, и наоборот (см. рис. 6, 7), скорости перемещения цепочек u относительно потока будут равны [26]

(3)

При этом Γ – циркуляция этих вихрей.

Вихревая частота равна

(4)

а число Струхаля пропорционально частоте ν_v. Тогда, из формул (1) – (4) при заданной форме тела, а также скорости потока и циркуляции, следует, что

(5)

Формула (5) объясняет увеличение числа Струхаля для дорожки Кармана, образующейся на круговом цилиндре, при Re > 5·10⁶. В этом случае пограничный слой на поверхности тела становится полностью турбулентным, и, поэтому, точки его отрыва с поверхности, где зарождаются вихри, оказываются ближе к его продольной оси (параллельной вектору скорости набегающего потока), чем в ламинарном пограничном слое при 3·10² < Re < 3·10⁵ [28]. Это приводит к тому, что и расстояние h между сторонами дорожки Кармана уменьшается, а ее число Струхаля растет от величины St ≈ 0.2 до величины St ≈ 0.3. Для этого достаточно уменьшения ширины дорожки на ~ 20 %.

Также становится понятным различие между числами Струхаля при обтекании кругового цилиндра и пластинки, поставленной поперек потока. Вихри срываются с ребер пластинки, но не с крайних поперечных точек поверхности кругового цилиндра, а с точек на его поверхности, которые расположены ближе к его продольной оси (см. рис. 6). Число Рейнольдса течения, показанного на этом рисунке, составляет Re = 140, тогда для цилиндра St ≈ 0.17 (см. рис. 8). Это означает, что при одинаковых поперечных размерах цилиндра и пластинки начальная, и, соответственно, установившаяся на некотором расстоянии от препятствия ширина дорожки вихрей за цилиндром должна быть процентов на 10 меньше, и число Струхаля, соответственно, – процентов на 20 выше (влияние различия скоростей на число Струхаля намного более слабое, и в данном случае им можно пренебречь). Можно видеть, что вертикальное удаление точек вихреобразования от продольной оси цилиндра на рис. 6 действительно примерно равно 90 % от его радиуса.

Рассмотрим теперь формирование дорожки Кармана на бесконечно длинном в продольном направлении теле с плоскими гранями, как если бы тело, изображенное на рис. 7 продолжалось вправо до бесконечности. Вихри всегда возникают на передних ребрах этого тела, при этом верхняя и нижняя стороны дорожки Кармана этим телом оказываются разделены, а сами вихри проходят вдоль его боковых твердых поверхностей. В невязкой сплошной среде граничное условие непротекания на твердой поверхности, как известно, может быть смоделировано с помощью отражения особенностей потока, то есть в рассматриваемом случае – вихрей [26]. Отражение вихрей должно производиться симметрично относительно этой твердой поверхности. Поэтому в математической модели, описывающей движение вихрей вдоль нее, появится цепочка фиктивных вихрей, которая вместе с реально существующей цепочкой в потоке образуют дорожку Кармана с симметричным расположением вихрей. И именно взаимодействие вихрей в каждой из этих двух новых дорожек Кармана определит их параметры.

Известно, что симметричное расположение вихрей является неустойчивым [26]. Это означает, что такие дорожки вихрей должны «рассыпаться» вскоре после своего образования, и, следовательно, число Струхаля для такого течения можно принять равным 0. Естественно предположить, что на реальных телах прямоугольного поперечного сечения числа Струхаля St будут иметь промежуточные величины между полученными выше крайними значениями St для пластинки и полубесконечного тела. Для их оценки можно использовать подходящую интерполяционную формулу, построенную по какому-либо набору экспериментальных данных, параметром которой должно быть отношение поперечной длины тела b к его высоте d:

(6)

где St₀ – величина числа Струхаля для плоской пластинки, λ – удлинение тела b/d, f(λ) – функция, удовлетворяющая следующим условиям:

(7)

Условие равенства 0 производной функции f при λ = 0 введено для того, чтобы при 0 ≤ λ ~ 1 число Струхаля слабо зависело от этого параметра (что соответствует экспериментальным данным), а при λ >> 1 – чтобы функция f(λ) асимптотически приближалась к 0. При 1 < λ ~ 10 эта функция должна давать значения, достаточно близкие к экспериментальным.

V – Оценки параметров флаттера Такомского, Волгоградского и Саратовского мостов

Применим полученные результаты для оценки числа Струхаля при возбуждении колебаний Такомского моста во время его разрушения. Мост имел сплошную Н-образную (двутавровую) балку жесткости, высота боковых стенок которой составляла 2.44 м, на которой было расположено дорожное полотно шириной b = 11.9 м [10]. При добавлении 0.5 м на толщину полотна моста полный поперечный размер его пролета d можно оценить, примерно, в 3 м. В день, когда произошло его разрушение, мост при скорости ветра около 17 м/с начал совершать изгибные колебания. Примерно через час стопор основного несущего троса ослаб и еще в течение получаса при скорости ветра 18.8 м/с мост стал совершать более интенсивные изгибные колебания на частоте 0.6 Гц. Затем, после обрыва части подвесок мост внезапно изменил тип колебаний и перешел на изгибно-крутильные колебания с частотой около 0.2 Гц, и, по прошествии 30 минут таких колебаний он разрушился [13].

При полной высоте поперечного сечения моста d = 3.0 м и при скорости ветра v = 18.8 м/с частота собственных изгибных колебаний, и частота образования вихрей Кармана (вихревая частота) ν_e ≈ ν_v ≈ 0.60 Гц получается по формуле (1) при числе Струхаля St = 0.096. Число Рейнольдса Re = 3.8·10⁶, и, как и ожидалось, из этих оценок можно сделать заключение, что и при таком числе Рейнольдса процесс срыва вихрей остается устойчивым. Так как произошел срывной флаттер, собственные частоты колебаний пролета в начале всего процесса при запуске автоколебаний были близки к вихревым частотам возбуждения, но вычисление собственных частот мостов выходит за рамки данной работы.

Частота колебаний пролетов Волгоградского моста по данным [27] составляла ν_v = 0.42 Гц, ширина пролетного строения – b = 16 м. а его высота – d = 3.5 м. Скорость ветра по заключению экспертной группы находилась в пределах 15 – 17 м/с [9]. Если принять скорость ветра равной 16 м/с, то число Струхаля St = 0.092, а число Re = 3.6·10⁶ и практически совпадает с числом Рейнольдса, вычисленным для Такомского моста. Удлинение λ для Такомского моста равно 4.0, для Волгоградского моста λ = 4.6. В качестве функции f(λ) из формулы (6), удовлетворяющей условиям (7), можно выбрать следующую:

(6)

где q – коэффициент, обеспечивающий согласование аппроксимирующей функции с имеющимися экспериментальными данными. Тогда четыре имеющиеся экспериментальные точки ложатся на кривую (8) при q = 0.17 со среднеквадратичным отклонением около 2.5 %. По ней для квадрата в поперечном сечении St = 0.14, для Такомского моста St = 0.099, а для Волгоградского – St = 0.091.

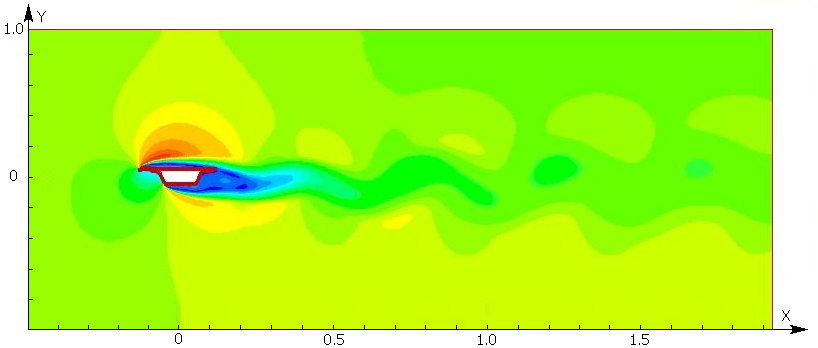Рис. 9

Хотя поперечное сечение Волгоградского моста не является прямоугольником (см. рис. 9), опираясь на данные, приведенные выше, будем считать это отличие при первичном анализе проблемы несущественным, так как расстояние h между вихрями в дорожке Кармана, определяющее число Струхаля, от этого практически не изменится. Имея большее количество экспериментальных точек, будет можно, если потребуется, скорректировать функцию f(λ) так, чтобы она лучше аппроксимировала экспериментальные данные в практически интересном диапазоне удлинений 0 < λ < 10.

На рис. 9 представлены также результаты и первых численных расчетов срывного обтекания пролетного строения Волгоградского моста, выполненные на кафедре Аэрогидродинамики Новосибирского государственного технического университета (НГТУ) под руководством проф. С. Д. Саленко. Показано поле скоростей. При скорости ветра 16 м/с (салатовый цвет), в окрестности пролета моста скорость потока изменяется от 2 м/с (темно-синий цвет) до 21.3 м/с (красный цвет). За пролетом видна дорожка Кармана.

Известно, что имеется близнец Волгоградского моста по конструкции пролетов – новый Саратовский мост. Его основная часть между правым берегом Волги и островом Котлубань (см. рис. 10) хоть и сильно отличается от Волгоградского моста по числу пролетов, однако их длина (за исключением крайних, расположенных у самых берегов или вообще полностью над землей) почти такая же: 10 пролетов по 126 м и 3 – по 157 м [5, 29]. Длинные судоходные пролеты расположены недалеко от острова. Первая очередь Саратовского моста (половина верхнего строения, как сейчас на Волгоградском мосту) была открыта 16 декабря 2000 года, а полностью в строй мост вошел в строй 16 октября 2009 года [30], через 6 дней после открытия первой очереди Волгоградского моста. Строительство второй очереди Саратовского моста велось с левого берега реки. Середина этого строительства по данным источника [31] приходится на зиму или начало весны 2009 года. Таким образом, оценка сверху продолжительности строительства второй очереди моста составляет не более полутора лет. Следовательно, в течение более 7 лет группа из трех пролетов длиной 157 м Саратовского моста находились примерно в том же состоянии, в каком аналогичные три пролета Волгоградского моста, попавшие в срывной флаттер через 7 месяцев после начала эксплуатации, находятся сейчас.

Рис. 10

Почему же за все эти годы на длинных пролетах Саратовского моста в отличие от Волгоградского моста не произошел срывной флаттер? Существуют два возможных ответа на этот вопрос. Первый предполагает, что слабые отличия в длине пролетов этих мостов (157 и 155 м), в граничных условиях для этой группы пролетов (у Волгоградского моста с одной стороны к этой группе прилегает пролет длиной 130 м, а у Саратовского моста – длиной всего лишь 84 м), а также возможные другие не слишком значительные конструктивные отличия привели к достаточно заметному сдвигу собственных частот колебаний длинных пролетов этих двух мостов. Второй ответ – за прошедшие годы Саратовский мост никогда не обдувался ветром с той скоростью, которая вызвала флаттер Волгоградского моста из-за различия их топографического окружения.

В глубине евразийского материка очень сильные ветры на значительных пространствах, как правило, бывают нечасто, а если они и наблюдаются, то, обычно в местах, топография которых способствует увеличению местной скорости ветра – во всяких складках и узостях геологических структур, оказавшихся параллельными направлению дующего ветра. Это увеличение скорости ветра в узостях, в принципе, следует из закона сохранения расхода потока сплошной среды. Ширина реки под Волгоградским мостом примерно в 4 раза меньше, чем под Саратовским (см. [5]). Справа от моста в Волгограде возвышается Мамаев курган. Слева от моста в Саратове начинается многокилометровая низменная пойма с большим количеством проток и озер, а у моста в Волгограде слева – поселения, и, следовательно, местность там должна быть выше. Таким образом, не исключена возможность того, что за прошедшие годы Саратовский мост не попал в срывной флаттер только потому, что никогда не обдувался ветром такой силы, какой она была 20 мая 2009 года в окрестности Волгоградского моста. Это предположение должны подтвердить или опровергнуть данные из архивов местной метеостанции.

После того, как верхнее строение Саратовского моста стало состоять из двух полос, изменились и его флаттерные характеристики. В частности, удвоение ширины пролетного строения привело к двукратному увеличению удлинения λ, и соответственно, снижению числа Струхаля и вихревой частоты по формуле (8) более чем вдвое. Поэтому теперь для совпадения собственной частоты колебаний моста и частоты внешнего возмущения требуется гораздо бόльшая скорость ветра.

VI – Инцидент с Витебским мостом и гасители колебаний

Несмотря на утверждения о том, что инцидент с Волгоградским мостом был первым, когда возникли сильные ветровые колебания балочного моста [6], не слишком сложно оказалось найти информацию об одном подобном случае, закончившемся намного более печально, чем растиражированный средствами массовой информации эпизод с «танцующим мостом». За 3.5 года до инцидента в Волгограде, 27 декабря 2006 года около 17 часов после окончания рабочей смены произошло обрушение строящегося моста через реку Западная Двина на юго-западном обходе Витебска [32]. Этот мост строился по новой технологии: металлические конструкции собирались на берегу, а затем надвигались на бетонные опоры. 26 декабря это было сделано, а на следующий день пролет моста длиной 126 м сломался пополам и упал в реку (см. рис. 11). Доступ к месту происшествия сразу же был закрыт – на расстоянии примерно полутора километров от недостроенного моста было установлено оцепление [33]. В прессе после первых кратких сообщений об аварии никакой информации более не появилось, однако, стало известно, что подул ветер, и, вследствие вихревого возбуждения развились колебания конструкции. Когда в корне балки прирост напряжений достиг 120 МПа, она сломалась [34].

Рис. 11

Место строительства моста за несколько месяцев до аварии показано на рис. 12. Следует отметить, что берега Западной Двины в этом месте довольно крутые и высокие (см. рис. 11), а мост строился там, где возвышенности, расположенные на обоих берегах реки, сближаются, увеличивая местную скорость ветра.

Рис. 12

Несмотря на отсутствие данных о скорости ветра, по имеющей информации вполне можно описать достаточно достоверную версию произошедшего. Для уменьшения массы консоли в то время, когда она надвигалась на опоры, у нее не была установлена верхняя плита. При этом снижение массы конструкции было достигнуто за счет значительно большего снижения ее жесткости на изгиб в горизонтальном направлении и на кручение. Из-за того, что в момент аварии пролет моста по существу представляла собой две сравнительно слабо связанные балки, площадь его горизонтальных поверхностей, на которые могла бы действовать заметная подъемная сила, была значительно меньше, чем была бы у пролета после завершения строительства. Однако аэродинамическая интерференция, возникающая при обтекании нескольких достаточно близко расположенных тел, приводит к возникновению на таких многобалочных конструкциях значительных изгибных колебаний в вертикальной плоскости поперек потока [35]. При этом в силу пространственного разделения элементов колебательной системы, по-видимому, более правильно говорить о бафтинге этого двухбалочного пролета.

Следует отметить, что технология надвижки пролета при постройке моста совершенно новой была только для белорусских мостостроителей. Еще в 1993 году при попытке надвижки трехбалочной консоли моста через реку Обь в Барнауле при скорости ветра 12 – 14 м/с возникли колебания размахом около 1 м, то есть примерно такие же по амплитуде, как и у Волгоградского моста [36]. Только в 1995 году после разработки и установки на консоли гребенок гасителей колебаний ее удалось поставить на место. Несмотря на простоту конструкции и скромные размеры гасители колебаний показали очень высокую эффективность: на всех скоростях ветра, вплоть до 25 м/с, колебаний конструкции не наблюдалось [36]. Аналогичные устройства использовались при монтаже пролетов моста через реку Томь в городе Томске (они хорошо видны над пролетом Томского моста на рис. 13), а также еще для нескольких мостов, построенных в Сибири [37]. Непонятно, почему эти гасители колебаний не использовались при монтаже пролета Витебского моста.

Рис. 13

Механизм работы этих гасителей колебаний прост и понятен: на щитах, по размерам существенно отличающихся от верхнего строения моста, формируются свои дорожки вихрей с другими частотами и скоростями движения [26], причем оси вращения у вихрей, срывающихся с боковой поверхности щитов перпендикулярны осям вращения вихрей, сходящих непосредственно с пролета. Вследствие всего этого вихри с разных дорожек Кармана «перепутываются» между собой, дорожки вихрей теряют устойчивость, и происходит крупномасштабная турбулизация ветрового потока. В целом, картина становится похожей на ту, которая имеет место при обтекании кругового цилиндра при числах Рейнольдса 5·10⁵ < Re < 5·10⁶ (см. раздел IV), когда число Струхаля невозможно определить. Другими словами, имевшийся без гасителей колебаний спектр вихрей одной дорожки Кармана, близкий к монохроматическому, «размазывается» по широкому диапазону частот с резким снижением максимальной спектральной амплитуды колебаний. Очевидно, что из-за этого сильно (на порядок) снижается возбуждение системы на частоте ее собственных колебаний, если до этого была резонансная близость между ней и возбуждающей частотой [37].

VII – Индекс аэроупругой устойчивости мостов

Из сказанного в предыдущих разделах следует, что срывной флаттер – это автоколебательный процесс. Взаимодействие вихрей Кармана с колеблющимся телом обеспечивает положительную обратную связь в колебательной системе. «Чаще всего срывной флаттер возникает тогда, когда одна из собственных частот колебаний тела близка или кратна частоте срыва вихрей с этого же тела в случае, когда оно неподвижно» [22]. Срывной флаттер начинается, когда скорость ветра превышает некоторое критическое значение. Следовательно, возбуждение автоколебаний в этом процессе – жесткое [38]. Таким образом, несмотря на иной механизм создания возбуждающих колебаний в этом процессе по сравнению с автоколебаниями воды в напорных системах гидроэлектростанций, здесь также вполне уместно использование индекса устойчивости, при превышении критического значения которого происходит возбуждение автоколебаний [4]. В данном случае его можно назвать индексом аэроупругой устойчивости. Применение индекса гидроакустической устойчивости к напорным системам гидро- и гидроаккумулирующих станций привело к прекрасному согласованию его величины и наблюдаемого поведения их гидроагрегатов [4, 39 – 42].

Формула, по которой вычисляется индекс устойчивости σ, одинакова для оценки возбуждения любого автоколебательного процесса, при котором уровень внешних возмущений остается постоянным [4, 41, 42]:

(9)

где θ – добротность колебательной системы в невозбужденном состоянии, ν_p – частота возбуждения, ν_e – частота собственных колебаний системы, k_σ – нормировочный (калибровочный) множитель, введенный для удобства использования индекса, m – кратность частот, z – зональный коэффициент, k_s – коэффициент состояния системы, f – функция. При первой реализации данной теории – гидроакустической, f(θ) ≈ θ, а нормировочный множитель, выбирался по экспериментальным данным так, чтобы граница между зонами устойчивости (не возбуждения) и неустойчивости (возбуждения автоколебаний) находилась при уровне σ ≈ 1. Удобно так поступать и в дальнейшем. Величина нормировочного коэффициента в различных автоколебательных процессах может быть разной, и ее определение является основной задачей в теории устойчивости описываемого типа. Множитель m в формуле (9) введен не только под знак модуля, но и в числитель ее первого сомножителя в связи с тем, что возбуждение автоколебаний при m ≠ 1 происходит в m раз реже, чем при m = 1, тогда его воздействие должно быть в m раз слабее, и, соответственно, индекс устойчивости в m раз больше.

Зональный коэффициент z используется, когда у колебательной системы в пространстве параметров существует более одной резонансной зоны с различающимися характеристиками (см. [41]). Впрочем, для срывного флаттера его всегда можно принимать равным 1 и исключить из формулы (9), так как механизм генерирования вихрей един во всей области возбуждения флаттера. Далее, вследствие того, что флаттер мостов может быть возбужден только на частоте вихрей Кармана или кратной ей, частоту возбуждения ν_p можно заменить вихревой частотой ν_v. Надо также учесть, что ветровая нагрузка, действующая на единичную длину моста, пропорциональна скоростному напору. Тогда формула (9) для рассматриваемого случая срывного флаттера должна измениться следующим образом:

(10)

где p – давление, ρ – плотность воздуха, v – скорость ветра. Верификация этой формулы должна производиться по экспериментальным данным, полученным для мостов, попадавших во флаттер.

При этом типичная величина добротности стальных мостов

где β – логарифмический декремент для балок без верхнего строения может быть порядка 200 [35], а завершенных пролетов (видимо, с асфальтобетонным покрытием) – на порядок ниже [43], что уже близко к добротности напорной системы Саяно-Шушенской ГЭС (θ = 18 – 22.5 в зависимости от режима и/или величины напора) [40]. По-видимому, функцию f(θ) можно аппроксимировать степенной зависимостью от добротности θ: f(θ) ~ θ^γ, и определить показатель степени γ из экспериментальных данных. А если добротность рассматриваемых мостов примерно постоянна, то может оказаться, что f(θ) ≈ const, и тогда ее просто будет можно включить в нормировочный множитель k_σ.

Коэффициент состояния системы k_s в нормальных (проектных) условиях работы системы равен 1, если нет прямых указаний на то, что данная система в данный момент чем-то отличается от систем со стандартным уровнем характеристик. Например, балки Витебского моста сразу после надвижки вследствие того, что ее поперечный контур был еще незамкнутым, должны были иметь меньшую изгибную и крутильную жесткости, чем пролеты других мостов такого же типа после завершения строительства. Поэтому коэффициент состояния k_s этого моста при вычислении по формуле (10) должен отличаться от коэффициента k_s мостов, уже находящихся в эксплуатации, и, видимо, быть меньше, чем у последних. Значения этого коэффициента могут быть определены из сравнения жесткости балок в обоих рассматриваемых состояниях и сил, действующих на них, или из статистических экспериментальных данных о критической скорости флаттера для балок мостов, находящихся в двух различных состояниях.

Использование формулы (10) для оценки возбуждения срывного флаттера возможно только при определении собственной частоты колебаний и добротности системы в условиях отсутствия внешних возмущений (частота возбуждения флаттера оценивается по формулам (1, 6, 8)). В простейших случаях, например, при колебаниях пролета моста с закрепленными концами или струны, видимо, можно получить достаточно точную оценку этих параметров с помощью аналитических методов. По-видимому, так может обстоять дело при оценке флаттерной устойчивости Такомского и Витебского мостов. Однако для более сложных случаев, например, таких как одновременные колебания сразу нескольких пролетов Волгоградского моста с не вполне ясными условиями связи пролетного строения с опорами, видимо, возможны только численные методы расчета, эксперименты на маломасштабных моделях и, наконец, натурные испытания, способ проведения которых описан в следующем разделе работы.

VIII – Действия, которые необходимо провести для повышения аэроупругой устойчивости мостов

Итак, при описываемом в разделе VII подходе по оценке флаттерной опасности мостов необходимо с помощью продувок в аэродинамических трубах получить зависимости числа Струхаля от удлинения тел, моделирующих пролетные строения мостов при 0 < λ < 10. Пока это не сделано, можно использовать оценку (10).

Необходимо также с помощью расчетов или экспериментов на маломасштабных подобных моделях определить частоты и добротности собственных колебаний мостов, которые разрушились или испытали сильные колебания при срывном флаттере. К таковым относятся Такомский, Витебский (без верхнего строения) и Волгоградский мосты, новые мосты в Барнауле и в Томске (при том же выносе консоли, что была тогда, когда там возникал или без гасителей колебаний мог возникнуть флаттер) и, может быть, еще некоторые другие. Кроме того, необходимо сделать то же самое для нескольких современных мостов облегченного типа, не испытавших флаттера, в первую очередь, для нового Саратовского моста. Все это надо осуществить при отсутствии внешних ветровых воздействий, что сильно облегчает как проведение расчетов, так и экспериментов. После этого будет возможно определить нормировочный множитель k_σ из формулы (10) для аэроупругой устойчивости, и тогда возникнет возможность ее быстрой оценки для любого моста.

Однако, для существующих мостов самым быстрым, точным и, видимо, наиболее простым способом получения этих данных являются натурные испытания. Достаточно, чтобы на мост въехал самоходный сейсмический вибратор, один которых изображен на рис. 14, и там же был установлен набор сейсмических приемников (см. [44]). После этого во время штиля или при достаточно слабом ветре, когда вынужденные колебания моста отсутствуют, следует определить спектр частот собственных колебаний нужных секций моста и скорость затухания этих колебаний. Видимо, все это легко могут проделать ближайшие к объекту геофизические службы. После этого, в частности, станет ясно, нужно ли что-нибудь делать с новым Саратовским мостом.

Рис. 14

Проделав эти эксперименты, можно подобрать гребенки щитовых гасителей флаттера для Волгоградского моста (хотя, по мнению некоторых специалистов, он «безнадежен» [14], но, на самом деле, скорее безнадежны такие специалисты), и, в случае необходимости, для нового Саратовского моста, а также для всех других современных мостов облегченного типа, где это будет нужно. После этого можно быть уверенным, что флаттерных проблем у этих мостов больше не будет. Кроме того, необходимо законодательно обязать мостостроителей использовать эти гасители при надвижке пролетов во время монтажа мостов.

Выводы

Колебания Волгоградского моста произошли под действием ветра в процессе возникновения срывного флаттера.
Формулы, следующие из теории вихрей Кармана, при использовании экспериментальной поправки позволяют рассчитывать частоту вихревого возбуждения моста с достаточной для оценок флаттера степенью точности.
Значительные ветровые колебания балочных мостов происходили и до инцидента с Волгоградским мостом.
На основе теории гидроакустического возбуждения автоколебаний напорных систем предложена аналогичная теория аэроупругой устойчивости мостов.
Предложен комплекс работ, которые следует провести для определения аэроупругой устойчивости мостов.
В настоящее время существует простой и эффективный способ полного устранения ветровых колебаний мостов с помощью гребенок щитовых гасителей флаттера, который следует использовать в случае возникновения такой необходимости.
При надвижке пролетов во время монтажа мостов использовать гребенки щитовых гасителей флаттера следует всегда.

Ссылки

Волгоградский мост. Wikipedia //
http://ru.wikipedia.org/wiki/Волгоградский_мост
Эксперты пришли к выводу, что Волгоградский мост находится в идеальном состоянии. ПолитРу //
http://www.polit.ru/news/2010/05/24/most.html
Ю. И. Лобановский – Технические причины катастрофы на Саяно-Шушенской ГЭС (итоги расследования), ноябрь 2009 //
http://synerjetics.ru/article/catastrophe.htm
Ю. И. Лобановский – Критерий возбуждения гидроакустических автоколебаний напорной системы, январь – февраль 2010 //
http://synerjetics.ru/article/excitation.htm
Яндекс. Карты //
http://maps.yandex.ru/
Уникальное явление. Взгляд, деловая газета, 21.05.2010 //
http://vz.ru/society/2010/5/21/404163.html
Волгоградский мост. Видео, 20.05.2010 //
http://www.youtube.com/watch?v=dM1rwdcFMG4
Б. С. Кисин, А. Н. Маринин – О причинах и следствиях нештатной ситуации на пролётных строениях моста через р. Волга в г. Волгограде. Комментарий кафедры «Мосты и сооружения на дорогах» Волгоградского государственного архитектурно-строительного университета //
http://www.bridgeart.ru/volgograd-most_misd/
Л. Бутузова – Расследование «Известий»: Танцующие с мостами. Известия, 28.05.2010 //
http://www.izvestia.ru/special/article3142349/
Такомский мост. Wikipedia //
http://ru.wikipedia.org/wiki/Такомский_мост
The Tacoma Narrows Bridge Collapse. Video, 07.11.1940 //
http://www.youtube.com/watch?v=j-zczJXSxnw
С. Кузьмина, П. Карклэ – Эолова арфа, самолеты и мосты. «Наука и жизнь», N 5, 2009 //
http://elementy.ru/lib/430811
E. T. de Grenet – Aerodinamica e vulnerabilità eolica per i ponti di grande luce. Dissertation, 2005 //
http://rzbl04.biblio.etc.tu-bs.de:8080/docportal/servlets/MCRFileNodeServlet/DocPortal_derivate_00004193/ediss.pdf
По мосту в Волгограде возобновляется движение легкового транспорта. Кавказский узел, 25.05.2010 //
http://www.kavkaz-uzel.ru/articles/169254/
Проектирование городских мостовых сооружений. МГСН 5.02-99 (07.09.1999 с изменениями от 19.08.2003 и 29.03.2005) //
http://www.docload.ru/Basesdoc/8/8233/index.htm
Живописный мост. Wikipedia //
http://ru.wikipedia.org/wiki/Живописный_мост
И что увижу, о том пою. Блог, 15.06.2010 //
http://vs259.blogspot.com/2010_06_01_archive.html
Муромский мост. Wikipedia //
http://ru.wikipedia.org/wiki/Муромский_мост
А. Бондарцев – Колебания волгоградского моста через Волгу. Livejournal //
http://abondarcev.livejournal.com/57338.html
Флаттер (авиация). Wikipedia //
http://ru.wikipedia.org/wiki/Флаттер_(авиация)
М. Ван-Дайк и др. Альбом течений жидкости и газа. Москва, «Мир», 1986 //
http://www.imec.msu.ru/content/nio/VanDaik/vd_main.html
П. С. Ланда – Срывной флаттер и эффект затягивания. Вестник научно-технического развития, N 6 (22), 2009 //
http://www.vntr.ru/ftpgetfile.php?id=308
Г. Фершинг – Основы аэроупругости. Москва, Машиностроение, 1984.
Воздух. Wikipedia //
http://ru.wikipedia.org/wiki/Воздух
Инженерный справочник. Таблицы DPVA.info //
http://www.dpva.info/Guide/GuideMedias/GuideAir/AirMaihHeatPropAndPrandtl/
Н. Е. Кочин, И. А. Кибель, Н. В. Розе – Теоретическая гидромеханика, т. I. М – Л, Гостехиздат, 1948.
С. Д. Саленко – Частное сообщение, 13.06.2010.
Л. Г. Лойцянский – Механика жидкости и газа. Москва, «Наука», 1978.
Мостовой переход через р. Волгу у с. Пристанное. Комментарий кафедры «Мосты и сооружения на дорогах» Волгоградского государственного архитектурно-строительного университета //
http://www.bridgeart.ru/bridge/pristan_bridge.php
Саратовский мост (новый). Wikipedia //
http://ru.wikipedia.org/wiki/Саратовский_мост_(новый)
Google. Карты //
http://maps.google.ru/maps?hl=ru&tab=wl
Н. Партолина – Под Витебском рухнул строящийся мост. Комсомольская правда в Белоруссии. 29.12.2006 Комсомольская правда в Белоруссии. 29.12.2006 //
http://news.tut.by/society/79828.html
В Республике Беларусь рухнул строящийся мост. Аварии мостов //
http://forum.bridgeart.ru/index.php?topic=238.0;wap2
Витебский мост. Дом физиков-романтиков //
http://club.foto.ru/forum/view_topic.php?topic_id=297897&page=2#listStart
С. Д. Саленко – Методика расчета аэроупругих колебаний многобалочных сооружений Прикладная механика и техническая физика, N 5, 2001.
Аэроупругость строительных конструкций. Сайт кафедры Аэрогидродинамики НГТУ //
http://craft.nstu.ru/agd/Scientific/Aerouprugost/Aerouprugost.html
S. D. Salenko – Technique of Multibeam Bridge Span Aeroelastic Oscillation Suppressing Proc. of XIth Intern. Conf. "Methods of Aerophysical Research", 1 – 7 July, 2002, Part 2, Novosibirsk.
Н. В. Карлов, Н. А. Кириченко – Колебания, волны, структуры. Москва, Физматлит, 2001.
Ю. И. Лобановский – Гидроакустическая устойчивость гидроаккумулирующих станций. Январь 2010 //
http://synerjetics.ru/article/stability.htm
Ю. И. Лобановский – Сопоставление расчетных и натурных данных в области гидроакустической неустойчивости напорных систем и на переходных режимах. Май 2010 //
http://synerjetics.ru/article/comparison.htm
Ю. И. Лобановский – Гидроакустический бустинг – способ возбуждения катастрофических автоколебаний в напорной системе Саяно-Шушенской ГЭС. Май 2010.
Ю. И. Лобановский – Тайна горной долины. Июнь 2010 // http://synerjetics.ru/article/pamir.htm
И. Каримов – Лекции. 14.1. Предмет и задачи динамики сооружений. Башкирский государственный аграрный университет //
http://www.stroitmeh.ru/lect51.htm
А. Бусыгин – Откуда берется нефть. Русский обозреватель. 27.01.2009 //
http://www.rus-obr.ru/discuss/1749

Благодарности - Автор выражает свою благодарность Д. В. Степанову, О. В. Федяеву и, особенно, С. Д. Саленко за полезные обсуждения и участие в работе.

Внутренняя Колыма,

30.06.2010 Ю.И. Лобановский