|
|
 |
| |
Критерий возбуждения
гидроакустических автоколебаний
напорной системы
|
| Ю.И.Лобановский |
|
Памяти 75 погибших в катастрофе Саяно-Шушенской ГЭС посвящается.
|
|
|
Краткое содержание
|
|
В работе рассмотрено
возбуждение гидроакустических автоколебаний в напорных водоводах
гидроэлектростанций с высокими плотинами. Если этот процесс развивается
при расходах воды бóльших, чем ее расход на рабочем режиме, то
происходит практически неограниченный рост пульсаций давления в
водоводе. Именно автоколебания явились причиной катастрофы на
Саяно-Шушенской ГЭС 17 августа 2009 года, а также аварии на Нурекской
ГЭС 9 июля 1983 года. |
|
Построена теория локального подобия для натурных
радиально-осевых гидравлических турбин средней и большой мощности,
позволяющая пересчитывать частоты прецессии затурбинного вихря с одной
турбины на другую (пульсации давления этой частоты, обычно, и
инициируют развитие автоколебаний). На основе решений волнового
уравнения с разрывным граничным условием, моделирующим турбину,
сравнения полученных в этих решениях собственных частот с частотами
возбуждения и учета логарифмических декрементов затухания выведен
критерий возбуждения автоколебаний для определения гидроакустической
устойчивости ГЭС. Вычислены индексы гидроакустической устойчивости
девяти гидроэлектростанций различных типов. К списку из двух
гидроэлектростанций, продемонстрировавших гидроакустическую
неустойчивость на практике, добавлены ГЭС на границе устойчивости и
неустойчивый расчетный вариант еще одной гидроэлектростанции. |
| Ключевые слова:
катастрофа – авария – Саяно-Шушенская ГЭС –
Нурекская ГЭС – высоконапорная плотина – гидроагрегат – турбина –
подобие – автоколебания – устойчивость – гидроакустический резонанс –
собственная частота колебаний – вихревая частота – турбинная частота –
моды колебаний – жесткое возбуждение – критерий возбуждения |
| |
ТАБЛИЦА СИМВОЛОВ
|
- c – скорость звука
- v – скорость потока
- t – время
- g – ускорение свободного
падения
- ω – угловая скорость
вращения
- p – давление
- ρ – плотность
- L – длина
- H – высота
- h – напор
- D – диаметр
- R – радиус
- M – момент сил
- W – мощность
- E – энергия
- Q – объемный расход
- q – безразмерный
расход, плотность потока энергии
- S – площадь
- x – пространственная
координата
- α – угол (атаки)
- μ – динамический
коэффициент вязкости
- η – эффективность
(коэффициент полезного действия)
- ν – частота
- Γ – циркуляция
- γ – безразмерная
циркуляция
- ζ – относительная
циркуляция
- ξ – параметр
оптимальности турбины
- κ(q) – безразмерная
функция, соответствующая стационарной характеристике турбины
- χ(q) – нормированная
производная функции κ(q)
- Φ – потенциал
скорости
- k – волновой вектор
- φ – действительная
часть волнового вектора
- ψ – мнимая часть
волнового вектора
- i – мнимая единица
- λ – длина волны
- ς – удельное
акустическое сопротивление
- δ – коэффициент
затухания
- β – логарифмический
декремент затухания или логарифмический инкремент возрастания (в
зависимости от его знака)
- θ – добротность
колебательного контура
- ε – отклонение
- N – натуральное
число, номер моды
- σ – индекс
устойчивости
- Re – число Рейнольдса
- Δ – символ разности
|
|
|
Индексы нижние
|
|
- 0 – невозмущенный
- b – излучательный
- с – расчетный
- d – диссипативный
- e – собственный
- eq – эквивалентный
- g – относящийся к
электрогенератору
- i – при постоянной
эффективности
- L – линейный,
определенный по длине L
- m – максимальный
- p – возбуждающий
- r – роторный
(турбинный)
- v – вихревой
|
|
|
Индексы верхние
|
|
- * –
характерный
- + –
за разрывом
- – –
перед разрывом
|
|
I – Введение
|
|
Как известно, 17 августа 2009 года в 8 часов 13 минут по
местному времени на Саяно-Шушенской гидроэлектростанции им. П. С.
Непорожнего (СШ ГЭС) из турбинного колодца на высоту около 14 м был
выброшен второй гидроагрегат, который незадолго до этого персонал
станции попытался остановить (см. [1 – 4]). Во время инцидента
произошло полное разрушение гидроагрегата. Его авария привела к
катастрофическому развитию событий на станции. Вода, под большим
давлением хлынувшая из открытого турбинного колодца, разрушила часть
конструкций машинного зала и уничтожила важнейшие подсистемы других
агрегатов, что привело к выходу их из строя и частичному или полному
разрушению. Машинный зал и помещения под ним были затоплены. К 9 часам
20 минутам с гребня плотины вручную были закрыты аварийно-ремонтные
затворы на водоводах всех гидроагрегатов и, таким образом, был
прекращен доступ воды с верхнего бьефа в машинный зал [1, 5]. |
|
Погибло 75 человек из персонала станции [6]. Внешний осмотр,
проведенный несколько дней спустя, показал, что второй, седьмой и
девятый гидроагрегаты разрушены, первый и третий получили серьезные
повреждения, четвертый, пятый, восьмой и десятый агрегаты имеют
незначительные повреждения, шестой (стоявший на ремонте) – находится в
удовлетворительном состоянии [1]. Эти предварительные оценки состояния
гидроагрегатов затем были уточнены, и в итоге ОАО «Силовые машины»
будет должно изготовить в течение 2010 – 2011 годов для Саяно-Шушенской
ГЭС «10 новых турбин, 9 гидрогенераторов, а также 6 систем возбуждения»
[7]. Таким образом, неповрежденным остался только один
электрогенератор, а все остальное основное гидроэнергетическое и
электрогенерирующее оборудование при проведении
ремонтно-восстановительных работ будет заменено, не говоря уже о том,
что в ходе этих работ в настоящее время производится разборка
разрушенного оборудования и восстановление машинного зала. |
|
С самого начала расследование катастрофы на СШ ГЭС стало сопровождаться
заявлениями официальных лиц о том, что произошло что-то уникальное и
необъяснимое, никогда не происходившее в практике гидроэнергетики [8,
9]. Спустя некоторое время в работе [3] на основе статей [10, 11] было
дано объяснение произошедшего: «второй гидроагрегат СШ ГЭС был разрушен
в результате впервые проявившегося в гидроэнергетике с такой мощью
сложного гидродинамического явления, которое в зависимости от
упрощенного способа его описания можно называть по-разному: помпаж
турбины, гидроакустический резонанс в напорной системе гидроагрегата,
автоколебательный процесс в водоводе, ряд возрастающих по интенсивности
неполных гидравлических ударов. Все эти названия в той или иной мере
описывают это страшное явление, не исчерпывая его полностью. Но
результат этого процесса очевиден – сорванная турбинная крышка, и
выброшенная из турбинного колодца в машинный зал центральная часть
гидроагрегата». |
|
После того, как была описана и понята причина катастрофы на СШ ГЭС,
естественно, возник вопрос: возможно ли ее повторение на других
гидроэлектростанциях? Кроме того, возникли сомнения в полной
уникальности этого инцидента. Ведь пульсации давления в водоводе
развиваются в каждом случае остановки и запуска гидроагрегата. Не было
ли в истории гидроэнергетики уже произошедших ранее случаев
возникновения автоколебаний, аварийных, но не катастрофических? |
В начале работы предполагалось, что для уверенного ответа на эти
вопросы, необходимо получить техническую документацию по гидроагрегатам
и водоводам достаточного количества высоконапорных гидроэлектростанций.
Затем надо было бы определить так называемые стационарные
характеристики турбин (зависимости между объемным расходом воды через
турбину и изменением на ней полного давления, см. [10, 11]), а также
получить доступ к данным по основным частотам пульсаций давления в
водоводах напорного тракта (см., например, [12]). После чего, решая
систему уравнений для потенциала скорости акустических колебаний в
напорном тракте и анализируя ее решения, вывести заключение о
возможности реализации и скорости роста пульсаций давления в напорных
трактах.
|
Однако это решение описывает только малые колебания, а практический
интерес вызывают большие пульсации
давления, в которых его изменения уже могут быть соизмеримыми с полным
перепадом давления воды на плотине ГЭС. Такие колебания перестают быть
линейными, и их характеристики при росте интенсивности
постепенно «уходят» от характеристик породивших их малых колебаний.
Поэтому, для получения окончательного заключения о возможности
катастрофического сценария усиления обычных пульсаций давления
умеренной интенсивности в водоводе на переходных («не рекомендуемых») и
«запрещенных» режимах работы гидроагрегата, представлялось необходимым
построить нелинейную теорию этого процесса, и после этого применить ее
к агрегатам нескольких потенциально опасных гидроэлектростанций.
Альтернативой или важным дополнением к этой работе могли бы быть
натурные испытания.
|
Очевидно, что описанная выше программа работ потребовала бы заметных
средств и большого времени. И нет никаких гарантий, что очередная
авария или даже катастрофа такого типа не произошла бы где-нибудь до ее
завершения. Поэтому представлялось желательным на первом этапе
попытаться упростить процедуру выявления потенциально опасных
гидроэлектростанций даже ценой снижения точности получаемых заключений.
После того, как с помощью упрощенной процедуры из десятков или,
возможно, сотен потенциально опасных объектов будут выявлены единицы
или, может быть один – два десятка гидроэлектростанций, входящие в
группу риска, к ним уже можно было бы применить описанную выше
полноценную программу исследований.
|
В процессе создания этого упрощенного способа оценки появилась теория
определения критерия возбуждения автоколебаний в водоводах напорных
гидроэлектростанций, позволяющая понять, относится ли данная ГЭС к
группе риска, то есть к тем станциям, у которых в напорном водоводе
возможно катастрофическое нарастание пульсаций давления, или нет. И
только для тех случаев, когда характеристики водовода находятся на
грани устойчивости и неустойчивости подобного процесса, необходимо
развернуть ту программу исследований, о которой было написано выше. При
этом можно указать, на каких станциях, и даже на каких гидроагрегатах
ее надо проводить в первую очередь.
|
Таким образом,
описанная в этой статье полуэмпирическая теория в значительной степени
уже решает задачи, поставленные здесь двумя – тремя абзацами выше, а
также нацеливает программу расширенных и уточняющих исследований именно
туда, где они могут принести наибольшую пользу, резко сократив затраты
и сроки их выполнения.
|
|
II – Условия возникновения
опасного роста пульсаций давления в водоводе
|
Наиболее формализованный подход к рассмотрению процесса
возникновения сильных пульсаций в напорном водоводе, хорошо описывающий
этот процесс, особенно в его начальной стадии, – это теория
гидроакустического резонанса [10, 11]. Из нее следует, что для того,
чтобы пульсации давления возрастали во времени, необходимо выполнение
двух условий:
- На стационарной
характеристике
турбины должен существовать падающий участок, где производная полного
давления по расходу отрицательна.
- Частота прецессии вихря в
напорном водоводе или частота других достаточно мощных источников
колебаний давления и собственные частоты колебаний воды в водоводе
должны быть близки между собой.
|
|
Как правило, на средних и мощных высоконапорных гидроэлектростанциях, в
том
числе и на Саяно-Шушенской ГЭС, используются радиально-осевые турбины
Френсиса с лопастями фиксированной геометрии. Из рассмотрения процесса
возникновения отрывных зон на таких лопастях в форме несимметричного
вращающего отрыва на турбине следует неизбежность образования за ней на
нерасчетном режиме работы вихря [3] с вращающимся (прецессирующим)
кавитационным шнуром [10, 11]. Это вызывает частичное запирание канала
и увеличивает потери полного давления при расходах как больше, так и
меньше номинального (расчетного). Из эксперимента известно, что при
совсем малых расходах потери хоть и выше, чем на расчетном режиме, но
все же ниже, чем на промежуточных. Отсюда следует, что на стандартной
стационарной характеристике радиально-осевой турбины должно быть не
менее двух падающих участков. Такие участки имеются в так называемых
областях II и IV «не рекомендованной» и/или «запрещенной работы» [5,
12], и первое необходимое условие усиления колебаний давления в трактах
гидроагрегатов с радиально-осевыми турбинами выполняется всегда. |
Второе же условие с достаточной для быстрого роста пульсаций точностью
реализуется, к счастью, сравнительно редко. Частота прецессии вихря в
напорном водоводе (вихревая частота) νv зависит
от частоты вращения
ротора турбины νr и степени отставания
от ротора несимметричного
вращающего отрыва, которая определяется особенностями обтекания
турбины. Частота собственных колебаний воды в водоводе νe
зависит от
его геометрии и с частотой вращения турбины прямо не связана. Поэтому
сильный гидроакустический резонанс, опасный для гидроагрегата, возможен
только при стечении неблагоприятных обстоятельств, что возможно, если
параметры, чрезмерное сближение которых и вызывает резонанс, не
контролируются при проектировании и эксплуатации гидроэлектростанции,
как это и было до сих пор всегда.
|
Поэтому, для предварительного решения поставленной задачи достаточно
найти гидроэлектростанции, для которых выполняется условие
|
|
|
где νp = νv
или νp = νr,
причем, как показали дальнейшие расчеты, в большинстве случаев, в том
числе и в обоих инцидентах, произошедших в реальности,
опасной оказывается близость частот собственной νe
и вихревой νv.
Высшие гармоники возбуждающих колебаний этих типов (см., например,
[11]), интенсивность которых ниже интенсивности колебаний
основной частоты, здесь во внимание не принимаются. Необходимая для
создания опасной ситуации точность выполнения условия (1), описываемая
введенным в работе индексом устойчивости, будет рассмотрена далее.
|
|
III – Применение теории
размерностей для анализа характеристик гидротурбин
|
Рассмотрим особенности обтекания турбины, которые важны для определения
вихревых и собственных частот колебаний потока воды. Хотя вязкость
является необходимым условием для возникновения отрыва, на его
начальной стадии, как это часто делается в аэродинамике [13], будем
рассматривать в целом невязкое течение, в котором малые зоны отрыва
хоть и оказывают на него некоторое воздействие, но являются неким
внешним фактором [13, 14].
|
|
Поэтому, для анализа основных характеристик гидротурбин используем
классическую формулу Эйлера (см., например, [15]), справедливую, строго
говоря, для невязкого потока |
|
|
| где M – момент сил, действующих
на ротор турбины, ρ – плотность жидкости, Q – ее объемный расход, ΔΓ –
изменение циркуляции потока жидкости на турбине. В простейшем случае
плоского обтекания профиля циркуляция Γ представляет собой контурный
интеграл от скорости потока на его поверхности. |
Так как мощность W турбины равна
|
|
|
| где ω – угловая скорость ее
вращения, то из выражений (2) – (3) следует, что |
|
|
| В потоке воды, текущем по
напорному водоводу, завихренность отсутствует, если пренебречь
относительно слабым влиянием на течение его стенок через вязкое
взаимодействие. Поэтому, можно считать, что циркуляция потока там равна
0. В направляющем аппарате радиально-осевой турбины поток ускоряется и
закручивается, и циркуляция Γ1 на выходе из него
максимальна. В турбине
поток раскручивается, и на выходе из нее циркуляция Γ2
на расчетном
режиме снова практически равна 0. Таким образом, в этом случае |
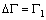 |
| На нерасчетных режимах из-за
отрывов на лопастях, приводящих к изменению завихренности потока,
некоторая доля от исходной циркуляции в потоке за турбиной остается. |
|
Если заменить угловую скорость вращения ротора турбины ω на более
удобную
для дальнейших применений частоту вращения ротора νr
|
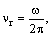 |
| то формула (4) может быть
преобразована к виду |
|
|
|
Так как размерность циркуляции [Γ] = м2/с, то, в
соответствии с теорией
размерностей (см., например, [16]) из выражения (5), можно получить
безразмерную величину циркуляции Δγ, используя характерную длину,
равную, например, диаметру ротора турбины D и характерное время,
равное νr–1: |
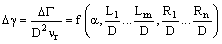 |
| как функцию только от
безразмерных параметров, где α – угол, характеризующий положение ротора
турбины по отношению к набегающему потоку, например угол атаки передних
кромок лопастей, L1…Lm и R1…Rn
– соответственно размеры и радиусы
кривизны, определяющие геометрию ротора, m, n – числа, при достаточных
наборах которых геометрия ротора турбины с помощью соответствующих длин
и радиусов описывается с необходимой степенью точности. |
Тогда
|
|
|
| Формула (6) означает, что при
подобии геометрии роторов различных турбин и при сохранении угла атаки,
под которым обтекаются лопасти, любые изменения размерных параметров,
имеющихся в формуле (6), и проводимые так, что их комплекс сохраняется
постоянным, не изменят величину безразмерной циркуляции Δγ. Все это
верно, если модель невязкой жидкости достаточно адекватно описывает
течение в окрестности ротора, что при отсутствии развитых отрывов на
его лопастях, обычно, является справедливым. |
Изучение изображений различных турбин Френсиса привело автора
этой работы к мысли, что их относительная геометрия (геометрия,
пересчитанная на один и тот же характерный размер) настолько
консервативна, по крайней мере, для рассматриваемой области параметров,
что в первом приближении ее можно считать постоянной. На основании
имеющегося у автора аэродинамического опыта было также высказано
предположение, что угол атаки на рабочем режиме от турбины к турбине
тоже мало изменяется. Из этого следует, что в первом приближении
функцию f(…) можно заменить константой. Строго говоря, для вихревых
течений, как известно, невозможно построить полноценную теорию подобия,
однако при рассмотрении течений с близкими масштабами в условиях только
зарождающегося влияния вязкости на течение в целом, применение этой
приближенной теории возможно. Правомерность и точность этого положения
будут проверены в разделе V работы с помощью сопоставления с
экспериментальными данными.
|
А сейчас, предполагая, что доказательство утверждения
|
|
|
| уже получено, выведем из него
полезное для дальнейшей работы следствие. Выражение (7) по существу
означает, что, пока оно выполняется, все роторы турбин после пересчета
на единый стандартный диаметр на рабочем режиме представляют собой одно
и то же («La nuit, tous les chats sont gris» – «ночью все кошки серы»).
Тогда, до тех пор, пока на лопастях не возникли достаточно развитые
зоны отрыва, то есть пока турбины не ушли слишком далеко от своих
рабочих режимов, все их остальные обезразмеренные параметры также
должны быть одинаковы. И хотя отрывное вихреобразование на лопастях
турбин вызвано вязкими процессами, но само их начало и интенсивность на
разных турбинах при выполнении условия (7), а также при приблизительном
равенстве чисел Рейнольдса, характеризующих эти агрегаты (см. раздел
V), должны быть подобными, инициируемые подобным невязким обтеканием. В
этих условиях предположение о том, что и вихревые частоты в этих
условиях также оказываются подобными, выглядит вполне приемлемым для
дальнейшей проработки. |
Вследствие того, что в рассматриваемой модели единственным масштабом
частоты является частота вращения ротора νr,
то вихревая частота в
напорном тракте водовода νv при
указанных выше условиях должна в первом
приближении быть пропорциональна ей:
|
|
|
| где νv
– искомая вихревая
частота, νr – частота вращения ротора
турбины, индекс * относится к
известным из эксперимента характерным значениям этих параметров.
Выражение (8) позволяет оценивать вихревые частоты различных
гидрогенераторов по величине этого параметра, известного хотя бы для
одного из них. Автору известны два набора вихревых частот для двух
режимов работы гидроагрегатов Саяно-Шушенской и Красноярской ГЭС [12].
Хотя вывод выражения (8) из условия (7) нельзя признать вполне строгим
вследствие того, что вязкость потока вполне может оказывать влияние на
возникновение и развитие колебаний, все-таки можно указать, что
пропорциональность различных лопаточных и лопастных, а также всех
других не слишком высоких частот величине νr
– частоте вращения ротора,
видимо, является вполне обыденным утверждением для любого
гидроэнергетика. Поэтому гидроэнергетическая практика в целом
подтверждает приемлемость рассматриваемого подхода (см., например,
[12]). |
Таким образом, после подтверждения адекватности выражения (7) и
определения границ его применения, алгоритм пересчета вихревых частот с
одной турбины на другую, по крайней мере, в условиях ограниченного
изменения масштабов, то есть при сравнении вихревых частот достаточно
крупных натурных турбин, становится ясным.
|
|
IV – Характеристики типичных
радиально-осевых гидротурбин
|
Рассмотрим основные характеристики агрегатов семи мощных и средних
гидроэлектростанций, оснащенных радиально-осевыми турбинами.
Используемая для дальнейшего анализа информация приводится в следующих
ссылках: Нурекская ГЭС – источники [17 – 20], Саяно-Шушенская – [3,
12], Чиркейская – [21], Гувер (Hoover) – [22 – 28], Итайпу (Itaipu) –
[29, 30], Красноярская ГЭС – [12, 31, 32], ГЭС Санься (Три Ущелья,
Three Gorges) – [33 – 35]. Наряду с ошибками, достаточно часто
приникающими в Интернет, и далее охотно тиражируемыми при многократном
копировании таких материалов в сети, используемые в некоторых случаях
источники информации страдали разрозненностью и фрагментарностью. Не
всегда было ясно, при каких условиях указываются те или иные параметры
гидроагрегата. Поэтому перед применением данных в дальнейших
приложениях, параметры должны быть проверены на взаимное согласование.
|
Основные энергетические параметры гидроагрегатов станций представлены в
таблице 1, где используются следующие обозначения: H – высота плотины,
h – напор воды в гидроагрегате на данном режиме работы, Q – объемный
расход воды, W – мощность электрогенератора, η – эффективность
(коэффициент полезного действия) гидротурбины по данным из приведенных
выше источников, ηc – расчетная эффективность
турбины, полученная по
другим параметрам. Эффективность турбины ηc
вычисляется по формуле
|
|
|
| где ρ – плотность воды, g –
ускорение свободного падения, ηg –
эффективность электрогенератора.
Величина ηg мощных и средних
электрогенераторов гидроагрегатов очень
высока и, обычно, находится в пределах 0.97 – 0.985 [36], поэтому при
расчетах по формуле (9) его значение в тех случаях, когда оно было
неизвестно, принималось ηg = 0.985. |
|
| Таблица
1 |
| N |
ГЭС |
H
(м) |
h
(м) |
Q
(м3/с) |
W
(МВт) |
ηс |
η |
|
| 1 |
Нурекская
- 1 |
300 |
223 |
155 |
310 |
0.928 |
– |
| 2 |
СШ - 2 |
245 |
220 |
315 |
640 |
0.956 |
| 3 |
СШ - 3 |
212 |
640 |
407.5 |
0.882 |
0.882 |
| 4 |
СШ - 4 |
326 |
640 |
0.958 |
0.958 |
| 5 |
СШ - 5 |
364 |
703.5 |
0.943 |
0.943 |
| 6 |
СШ - 6 |
389.5 |
742.5 |
0.931 |
0.931 |
| 7 |
СШ - 7 |
425 |
768 |
0.882 |
– |
| 8 |
Нурекская - 2 |
300 |
203 |
126.5 |
220 |
0.887 |
| 9 |
Нурекская - 3 |
118 |
200 |
0.863 |
| 10 |
СШ
- 1 |
245 |
194 |
358.5 |
640 |
0.952 |
| 11 |
СШ - 8 |
170 |
410 |
640 |
0.950 |
| 12 |
Чиркейская - 2 |
232.5 |
185 |
168 |
285 |
0.949 |
| 13 |
Чиркейская
- 1 |
170 |
160 |
250 |
0.951 |
| 14 |
Гувер |
221 |
156 |
96 |
130 |
0.898 |
0.900 |
| 15 |
Итайпу |
196 |
110.5 |
700 |
700 |
0.937 |
0.938 |
| 16 |
Красноярская |
124 |
93 |
615 |
500 |
0.911 |
– |
| 17 |
Санься |
181 |
80.5 |
996 |
700 |
0.904 |
0.900 |
|
|
Если в названии ГЭС
используются цифры, то они означают вариант режима гидроагрегата, при
этом цифра 1 всегда соответствует номинальному рабочему режиму. Если в
таблицах ГЭС встречается только один раз и не имеет дополнительных
цифровых обозначений, то данные относятся к номинальному рабочему
режиму. Характеристики на этом режиме выделяются в таблицах 1 – 5
жирным шрифтом.
|
Эффективность турбин η на рабочих режимах, как известно, меньше 1, но
достаточно высока. При работе гидроагрегатов СШ ГЭС на повышенном
напоре она близка к 0.96 [12]. При изменении напора в допустимых
пределах она изменяется мало (ср. данные по СШ ГЭС при номинальной
мощности 640 МВт и напорах 194 и 212 м [12]). Для менее напорных турбин
эта величина ниже и близка к 0.90 [28, 34], и, следовательно, на
рабочих режимах (в так называемой области допустимых режимов III (см.,
например, [12])) границы изменения эффективности турбин составляют
примерно 0.90 – 0.96. Поэтому контроль этой величины позволяет
определить взаимосвязь между напором, расходом и мощностью
гидроагрегата в тех случаях, когда они разрозненно приводятся в
различных источниках информации. Это, в первую очередь, относится к
данным из таблицы 1 для Чиркейской ГЭС (где, из-за близости схемы и
высоты ее плотины к плотине СШ ГЭС, было принято такое же
значение ηc
на номинальном режиме работы) и Итайпу (здесь через η было определено
значение напора h на номинальном режиме). Кроме того, таким образом
можно оценить характеристики гидроагрегата на других рабочих режимах,
что было использовано для оценок на режимах СШ ГЭС – 2 и СШ
ГЭС – 8,
которые соответствуют верхнему и нижнему граничным значениям напоров
для этих станций. Режим СШ ГЭС – 3 относится к области не
рекомендованной работы II с образованием сильных вихрей за турбиной, и
поэтому эффективность турбины в этом случае ниже 0.90 [12] и меньше,
чем на наиболее эффективных рабочих режимах на 7.5 – 8 %.
Режимы СШ
ГЭС – 6 и 7 относятся к области запрещенной работы IV, и там
эффективность турбины также быстро падает [12]. Аппроксимация этих
данных квадратичной зависимостью по безразмерному расходу (расходу воды
через турбину, отнесенному к номинальному расходу) позволила оценить
эффективность турбины на режимах Нурекская ГЭС – 2 и Нурекская ГЭС – 3,
которые относятся к области не рекомендованной работы II.
|
Максимальное значение эффективности получено на турбине
РО-230/833-0-677 СШ ГЭС – ηc = 0.95 –
0.96 в окрестности оптимума [12].
Более низкое значение ηc = 0.93 у
агрегата Нурекской ГЭС на Вахше,
по-видимому, вызвано в основном тем, что там используются гораздо более
длинные водоводы, расположенные не на боковой поверхности плотины как у
Саяно-Шушенской и Чиркейской ГЭС, а пробитые в скалах, окружающих очень
широкую насыпную гравитационную плотину Нурекской ГЭС, сбоку от нее.
Кроме того, первоначально вода там течет по 3 туннелям, которые, за 610
– 666 м до турбин делятся каждый на 3 водовода, создавая этим
дополнительные потери в потоке воды [18]. На станции Гувер на реке
Колорадо также используется водоводы, отходящие под углами, близкими к
прямым, от двух боковых туннелей [22], что должно быть основной
причиной самого низкого из всех рассмотренных значения эффективности η
= 0.90 [28]. Причины также относительно низкой эффективности менее
напорных турбин на Итайпу, Красноярской ГЭС и Санься обсуждаются далее.
|
Известно 4 основных типа гидротурбин на средние и большие мощности:
осевые пропеллерные турбины Каплана [37] и диагональные
турбины Дериаса [38] с управляемыми лопастями, а также
радиально-осевые турбины Френсиса [39] и ковшовые турбины Пелтона [40]
с фиксированной геометрией лопастей. Область их применения зависит, в
основном, от напора, но также и от расхода и мощности (см., например,
[41]). Однако, существует и комплексный эмпирический критерий
оптимальности выбора типа турбины [42]. Если от британских единиц
перейти в систему СИ, то есть, как и везде в этой статье, измерять
частоту νr в герцах, мощность W в
мегаваттах, а напор h в метрах, то
после умножения исходного выражения на 500, параметр оптимальности типа
турбины ξ численно полностью совпадет с его значениями в британской
системе единиц
|
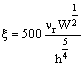 |
(можно считать, что коэффициент
500 имеет размерность, обратную размерности дроби, на которую он
умножается, тогда параметр ξ становится безразмерным). А в британской
системе единиц были выявлены следующие эмпирические закономерности
[42]: при 1 < ξ < 20 оптимальны ковшовые турбины, при 10
< ξ < 90 – радиально-осевые, 25 < ξ < 110 –
диагональные турбины [41 – 43], а при 70 < ξ < 260 –
осевые. Как известно, ковшовые турбины являются реактивными, то есть
они
преобразуют в работу потенциальную энергию жидкости, а осевые
– активными, использующими в основном, кинетическую энергию
потока.
Радиально-осевые турбины – это активно-реактивные агрегаты, причем на
нижней границе допустимой области изменения параметра ξ высока степень
их реактивности, а на верхней границе – соответственно,
степень активности, что сближает их там с осевыми
пропеллерными
турбинами.
Диагональные турбины представляют собой тип агрегатов, промежуточных
между радиально-осевыми и осевыми турбинами.
|
Значения параметра оптимальности ξ агрегатов с радиально-осевыми
турбинами для ГЭС, рассмотренных в таблице 1, при их работе на
номинальных режимах представлены в таблице 2 (здесь D – диаметр ротора
турбины):
|
|
| Таблица
2 |
| N |
ГЭС |
h
(м) |
W
(МВт) |
νr
(Гц) |
D
(м) |
ξ |
|
| 1 |
Нурекская |
223 |
310 |
3.33 |
4.75 |
34 |
| 2 |
СШ |
194 |
640 |
2.38 |
6.77 |
42 |
| 3 |
Чиркейская |
170 |
250 |
3.33 |
4.50 |
43 |
| 4 |
Гувер |
156 |
130 |
3.00 |
4.33 |
31 |
| 5 |
Гувер - М |
156 |
130 |
4.62 |
3.09 |
48 |
| 6 |
Итайпу |
110.5 |
700 |
1.53 |
8.45 |
57 |
| 7 |
Красноярская |
93 |
500 |
1.56 |
7.50 |
60 |
| 8 |
Санься |
80.5 |
700 |
1.25 |
9.71 |
69 |
|
|
Как известно, радиально-осевые
турбины могут применяться в диапазоне напоров 20 – 700 м [39, 41]. В
целом, за исключением турбины ГЭС Гувер, как и должно было бы быть для
турбин, спроектированных по единым принципам, при уменьшении
номинального напора h параметр ξ постепенно уменьшается от 34 до 69,
что уже близко к верхней границе допустимой области для
радиально-осевых турбин, и при напоре около 80 м (ГЭС Санься на Янцзы)
практически выходит на границу области работы осевых турбин.
|
Характеристики турбин для станции Гувер закладывались на 40 – 70 лет
раньше всех других рассматриваемых здесь агрегатов, и это, видимо,
объясняет, почему по параметру ξ эти турбины несколько выбиваются из
общего ряда. Их аналог, спроектированный по современным стандартам (с
учетом необходимости иметь целое число полюсов на электрогенераторе),
обозначен как Гувер - М и отличается только увеличенной чуть более чем
в 1.5 раза скоростью вращения и, соответственно, уменьшенными в 1.4
раза размерами, что должно было бы уменьшить массу и металлоемкость
ротора примерно в 2.5 раза. Параметр ξ модернизированного агрегата
возрос бы пропорционально увеличению частоты вращения, и этот агрегат
оказался бы в ряду современных машин. Из сказанного выше ясно, что
более низкие значения эффективности гидроагрегатов Итайпу, Красноярской
ГЭС и ГЭС Санься объясняются в первую очередь тем, что радиально-осевые
турбины их гидроагрегатов достаточно близки к границе допустимой
области использования, где они в принципе не могут работать также
эффективно как в ее середине.
|
Таким образом,
основные энергетические параметры агрегатов гидроэлектростанций, на
режимах, приведенных в таблице 1, можно считать выверенными, и они
могут быть использованы для дальнейшего анализа.
|
|
V – Определение границ
применения параметров подобия
|
Вычислим теперь параметр подобия Δγ (безразмерную циркуляцию турбины)
|
|
|
для агрегатов на этих режимах,
см. таблицу 3 (как и ранее жирным шрифтом выделены номинальные рабочие
режимы агрегатов).
|
|
| Таблица
3 |
| N |
ГЭС |
h
(м) |
Q
(м3/с) |
Δγ∙103 |
ζ |
ζi |
Δζ/ζ0 |
ηс |
|
| 1 |
Нурекская
- 1 |
223 |
155 |
8.12 |
1.230 |
– |
– |
0.928 |
| 2 |
СШ - 2 |
220 |
315 |
7.95 |
1.204 |
0.956 |
| 3 |
СШ - 3 |
212 |
640 |
7.14 |
1.083 |
1.176 |
0.080 |
0.882 |
| 4 |
СШ - 4 |
326 |
7.69 |
1.165 |
1.165 |
0.000 |
0.958 |
| 5 |
СШ - 5 |
364 |
7.56 |
1.145 |
1.163 |
0.015 |
0.943 |
| 6 |
СШ - 6 |
389.5 |
7.44 |
1.128 |
1.161 |
0.028 |
0.931 |
| 7 |
СШ - 7 |
425 |
7.07 |
1.071 |
1.163 |
0.079 |
0.882 |
| 8 |
Нурекская - 2 |
203 |
126.5 |
7.06 |
1.069 |
– |
– |
0.887 |
| 9 |
Нурекская - 3 |
118 |
6.88 |
1.042 |
0.863 |
| 10 |
СШ
- 1 |
194 |
358.5 |
6.98 |
1.058 |
0.952 |
| 11 |
СШ - 8 |
170 |
410 |
6.10 |
0.925 |
0.950 |
| 12 |
Чиркейская - 2 |
185 |
168 |
7.67 |
1.162 |
0.949 |
| 13 |
Чиркейская
- 1 |
170 |
160 |
7.06 |
1.070 |
0.951 |
| 14 |
Гувер |
156 |
96 |
8.15 |
1.234 |
0.898 |
| 15 |
Итайпу |
110.5 |
700 |
6.07 |
0.920 |
0.937 |
| 16 |
Красноярская |
93 |
615 |
6.03 |
0.914 |
0.911 |
| 17 |
Санься |
80.5 |
996 |
4.84 |
0.734 |
0.904 |
|
|
Для анализа результатов более
удобно отнести параметр подобия Δγ к некоторому характерному его
значению на рассматриваемом интервале для того, чтобы величина
безразмерной циркуляции была бы близка к 1:
|
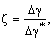 |
В таблице 3 показаны значения ζ
при Δγ* = 6.6∙10–3.
|
Эти же значения ζ на номинальных режимах агрегатов построены в таблице
4 по параметру ξ. Из нее можно видеть, что зависимость ζ(ξ) практически
является монотонной. Это означает, что снижение степени реактивности
радиально-осевых турбин и, соответственно, увеличение степени
их активности, приводят к такому постепенному дрейфу геометрии
их
роторов, которое вызывает уменьшение параметра безразмерной циркуляции
ζ. То, что зависимость ζ(ξ) более-менее монотонная, но не плавная,
означает, что конструирование эффективных и мощных турбин до сих пор,
по-видимому, не только наука, но отчасти еще и искусство.
|
|
| Таблица
4 |
| N |
ГЭС |
ξ |
ζ |
ζL |
ε
(%) |
|
| 1 |
Нурекская |
31 |
1.234 |
1.238 |
0.3 |
| 2 |
СШ |
34 |
1.230 |
1.200 |
– 2.4 |
| 3 |
Чиркейская |
42 |
1.058 |
1.105 |
4.5 |
| 4 |
Гувер |
43 |
1.070 |
1.089 |
1.7 |
| 6 |
Итайпу |
57 |
0.920 |
0.919 |
– 0.2 |
| 7 |
Красноярская |
60 |
0.914 |
0.870 |
– 4.8 |
| 8 |
Санься |
69 |
0.734 |
0.768 |
4.6 |
|
|
Была построена линейная аппроксимация зависимости ζ(ξ), при которой
среднеквадратичные отклонения от вычисленных значений ξ были бы
минимальными. Величины безразмерной циркуляции, вычисленные с помощью
этой линейной функции
|
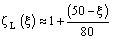 |
показаны в таблице 4 в столбце
ζL. Значения функции следующие: ζL(30)
= 1.25, ζL(50) = 1.00, ζL(70)
=
0.75. Среднеквадратичное отклонение значений этой функции от полученных
данных составляет 3.5 %, отклонения в заданных точках представлены в
столбце ε таблицы 4.
|
Отсюда видно, что параметр ζ, который при строгом выполнении законов
подобия должен быть постоянным, в рассматриваемом диапазоне изменения
размерных параметров турбин отклоняется от его среднего значения
примерно на ± 25 %. Такие отличия слишком велики, чтобы использование
законов подобия было бы практически полезным. Однако, если характерный
интервал 30 < ξ < 70 разбить на 2 части: 30 < ξ
< 50 (напорные радиально-осевые турбины) и 50 < ξ
< 70 (турбины умеренной напорности), максимальные отклонения
параметра подобия ζ от его средних значений составляют около ± 11 % на
первой половине интервала и около ± 14 % на его второй половине, что
уже вполне приемлемо для практических оценок. Как показали дальнейшие
исследования, для поиска опасных резонансных режимов, по крайней мере в
том случае, когда водоводы расположены на внешней поверхности плотины,
как у СШ ГЭС, представляет интерес только первая половина интервала 30
< ξ < 50, которая при типичных умеренных и больших
мощностях агрегатов (102 – 103
МВт) приблизительно соответствует
напорности в водоводах на номинальном режиме более 120 – 150 м, то есть
высоте плотины не ниже 175 – 200 м.
|
Следует сделать несколько замечаний о режимах работы турбин,
отличающихся от номинального (см. строчки таблицы 3 с индексами режимов
больше 1). Данные для режимов СШ ГЭС – 3, 4, 5 и 6 были
получены на
основании слегка скорректированных по формуле (9) на постоянный напор
212 м достаточно надежных результатов натурных экспериментов,
проведенных ранее на этой станции, см. [12]. Для этих режимов наряду с
безразмерной циркуляцией ζ по формулам (9) – (10) вычислена также
величина ζi при постоянном и максимальном
значении эффективности
турбины ηc = 0.958. Относительная
величина разности этих циркуляций
показана в столбце Δζ/ζ0 таблицы 3. В рамках
рассматриваемой модели
относительные потери циркуляции Δζ/ζ0 и потери
эффективности турбины
Δη/η0 совпадают.
|
Вследствие практически полного отсутствия отрывов потока на лопастях
турбины в малой окрестности номинального рабочего режима в середине
рабочей области III, величина коэффициента эффективности турбины
определяется минимально возможными диссипативными потерями в напорном
тракте и отсасывающей трубе, а также неустранимыми потерями на самой
турбине. При уходе турбины от оптимального режима на ее лопастях
возникают сначала небольшие, а затем все возрастающие зоны отрыва. Они
приводят как снижению эффективности турбины η, так и соответствующему
уменьшению коэффициента безразмерной циркуляции ζ (см. режимы СШ ГЭС -
3 – СШ ГЭС - 7 в таблицах 3, 5). При этом снижение перепада циркуляции
на турбине ΔΓ вызывает все возрастающую завихренность потока в
отсасывающей трубе и возникновение там вихря с кавитационным шнуром в
его центре (см., например, [11, 15]). Из того, что потери полного
давления в потоке Δp и снижение эффективности турбины Δη вызваны одной
и той же причиной – появлением и ростом отрывов на ее лопастях, в
окрестности номинальной рабочей точки в первом приближении можно
считать, что при малых изменениях этих параметров
|
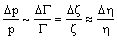 |
Тогда изменение потерь полного давления на турбине по расходу можно
пересчитывать для других агрегатов в соответствии с изменением их
эффективности η. На рис. 1 представлена обезразмеренная стационарная
характеристика турбины, то есть выглаженная экспериментальная кривая
(см. [10, 11]) относительных потерь полного давления Δp/p от
безразмерного расхода q = Q/Q* для десятого гидроагрегата СШ ГЭС на
номинальном напоре (Q* = 358.5 м3/с – объемный
расход воды на рабочем
режиме [44]). На этом рисунке в соответствии с подходом, использованным
в работах [10, 11], вертикальными пунктирными линиями выделены зоны, в
которых производная функции Δp/p (за исключением их границ) сохраняет
постоянный знак. На границах зон в точках экстремумов, производная
равна 0. Область малых расходов при q ≤ 0.45 не рассматривается как не
имеющая интереса для решения задач этой работы. В зонах A и A’
производная функции Δp/p отрицательна, в зоне B – положительна. Точки
перегиба на рис. 1 отмечены черными кружками. Пунктирная линия –
продолжение зависимости, полученное зеркальным отражением относительно
вертикальной оси, проходящей через точку максимума, отрезка
экспериментальной кривой в зоне B до точки перегиба. Далее наклон
пунктирной кривой начинает постепенно возрастать в соответствии с
увеличением наклона кривой η(q) (см. [12]). Более подробно поведение
стационарной характеристики турбины в зоне A’ описано в разделе VI.
|
|
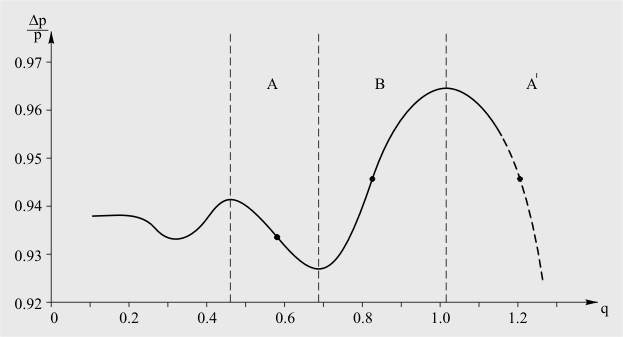 |
Рис. 1
|
|
Так как интересующий нас режим вихревого течения за турбиной обязан
своим происхождением вязкости, то необходимым условием правомерности
каких-либо пересчетов параметров с одного режима течения на другой
кроме подобия параметров невязкого течения является равенство или, по
крайней мере, близость чисел Рейнольдса на этих режимах. Вследствие
того, что плотность ρ и вязкость μ воды постоянны на всех
рассматриваемых режимах, числа Рейнольдса
|
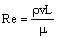 |
на различных агрегатах могут
отличаться только из-за изменения характерной скорости v и размеров L,
по которым эти числа Рейнольдса определяются. При выполнении условий
подобия
|
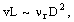 |
| поэтому, в рассматриваемой
ситуации |
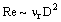 |
В итоговой для этого раздела таблице 5 кроме параметра подобия ζ
показаны также числа Рейнольдса Re для рассмотренных ранее агрегатов,
отнесенные к этому числу Re* для турбины Саяно-Шушенской ГЭС.
Максимальное изменение чисел Рейнольдса в рассматриваемом диапазоне
параметров агрегатов примерно двукратное. Такие вариации числа
Рейнольдса обычно слабо влияют на любые изменения технически значимых
параметров, если эти вариации не попадают в зону перехода ламинарного
пограничного слоя в турбулентный или какую-либо иную зону качественного
изменения течения [14]. Поэтому, за исключением особо неудачных для
моделирования ситуаций, которые вряд ли могут иметь место на
номинальных режимах работы турбин, можно считать, что числа Рейнольдса
для всех рассматриваемых агрегатов достаточно близки, чтобы при
дальнейших оценках можно было бы опираться на соотношения
подобия (7) – (8).
|
|
| Таблица
5 |
| N |
ГЭС |
h
(м) |
Q
(м3/с) |
η |
ζ |
Re/Re* |
|
| 1 |
Нурекская
- 1 |
223 |
155 |
0.93 |
1.23 |
0.69 |
| 2 |
СШ - 2 |
220 |
315 |
0.955 |
1.20 |
1.00 |
| 3 |
СШ - 3 |
212 |
640 |
0.88 |
1.08 |
| 4 |
СШ - 4 |
326 |
0.96 |
1.17 |
| 5 |
СШ - 5 |
364 |
0.94 |
1.15 |
| 6 |
СШ - 6 |
389.5 |
0.93 |
1.13 |
| 7 |
СШ - 7 |
425 |
0.88 |
1.07 |
| 8 |
Нурекская - 2 |
203 |
126.5 |
0.89 |
1.07 |
0.69 |
| 9 |
Нурекская - 3 |
118 |
0.86 |
1.04 |
| 10 |
СШ
- 1 |
194 |
358.5 |
0.95 |
1.06 |
1.00 |
| 11 |
СШ - 8 |
170 |
410 |
0.95 |
0.93 |
1.00 |
| 12 |
Чиркейская - 2 |
185 |
168 |
0.95 |
1.16 |
0.62 |
| 13 |
Чиркейская
- 1 |
170 |
160 |
0.95 |
1.07 |
0.62 |
| 14 |
Гувер |
156 |
96 |
0.90 |
1.23 |
0.52 |
| 15 |
Итайпу |
110.5 |
700 |
0.94 |
0.92 |
1.00 |
| 16 |
Красноярская |
93 |
615 |
0.91 |
0.91 |
0.80 |
| 17 |
Санься |
80.5 |
996 |
0.90 |
0.73 |
1.08 |
|
|
Тогда, из всего вышесказанного следует, что формула (8), где νv*
и νr*
соответствующие характерные частоты агрегатов Саяно-Шушенской или
Красноярской ГЭС, при выполнении условий подобия радиально-осевых
гидротурбин
|
|
|
может использоваться для оценки
вихревых частот гидроагрегатов
других станций, например, из рассматриваемого в таблицах 1 – 5 списка,
при ограничении отклонений параметров ζ и Re.
|
Конечно, частота
колебаний в напорном водоводе вследствие прецессии затурбинного вихря –
это характеристика процесса, на которую могут воздействовать и многие
другие неучтенные здесь факторы. Поэтому вполне достоверными данными
могут быть только данные эксперимента, о чем уже говорилось во
введении, и при развитии таких исследований просто необходимо
регистрировать эти частоты в водоводах гидроэлектростанций, внесенных в
группу риска по гидроакустическому резонансу. Однако, ограниченную
экспериментальную проверку соотношения (8) можно провести уже сейчас.
|
Известно, что частоты вращения роторов νr
турбин Саяно-Шушенской и
Красноярской ГЭС составляют, соответственно, 2.38 Гц [12] и 1.56 Гц
[32]. За турбиной СШ ГЭС минимальная жгутовая (вихревая) частота в
области не рекомендуемой работы II (см. [5, 12]), совпадающей с зоной A
и левой половиной зоны B на рис. 1, составляет 0.4 – 0.5 Гц, а за
турбиной Красноярской ГЭС – 0.32 Гц [12]. Пересчет по формуле (8) с
вихревой частоты СШ ГЭС приводит к значениям 0.26 – 0.33 Гц, что дает
отклонения от экспериментальной величины на 3 – 20 %. Здесь следует
отметить, что параметры подобия ζ для номинального режима (СШ
ГЭС – 1)
и режима в зоне II (СШ ГЭС – 3), а также для номинального
режима работы
Красноярской ГЭС (см. таблицу 5), отличатся на 15 – 20 %. Так что
полное согласование вихревых частот у агрегатов этих
гидроэлектростанциях было бы только простым совпадением. Примерно
аналогичная ситуация имеет место и для вихревых частот этих станций в
области запрещенной работы. В области IV (зоне A’) СШ ГЭС вихревая
частота νv = 1.40 – 1.45 Гц, а на
Красноярской ГЭС эта частота νv ≈ 1.2
Гц [12]. Пересчет по формуле (11) дает для вихревой частоты этой
станции значение νv ≈ 0.95 Гц, что
отличается от экспериментального на
те же 20 %. С учетом различия значений параметров подобия на 15 – 20 %
можно считать, что имеющиеся экспериментальные данные, по крайней мере,
не противоречат результатам теории подобия, описанной в разделах III –
V данной работы. При меньшем различии параметров подобия сравниваемых
агрегатов согласование их вихревых частот должно быть выше.
Своеобразная дополнительная экспериментальная проверка применимости
этой теории «ограниченного подобия» к рассматриваемым процессам
проведена также в разделе VIII при рассмотрении аварии на Нурекской ГЭС.
|
|
VI – Метод расчета собственных
частот водоводов
|
Итак, метод оценки вихревой частоты гидроагрегата νv
в областях II и IV
(зонах A, B и A’) дан. Теперь необходимо научиться определять
собственную частоту колебаний в напорном водоводе νe
даже в случае
минимума известной о нем информации. Как известно, бесконечно малые
колебания в напорном водоводе и в отсасывающей трубе,
диаметрами которых можно пренебречь по сравнению с их длинами (система
с одной степенью свободы), описываются одномерным волновым уравнением
для потенциала скорости Φ:
|
|
|
где x – единственная
принимаемая во внимание пространственная координата, t – время, c –
скорость звука в водоводе, p – давление, ρ – плотность воды.
|
На открытых концах водовода (поток течет слева направо, x = 0 – начало
напорного водовода, L – конец отсасывающей трубы) граничные условия
стандартные [45]:
|
|
|
где L1
– длина напорного
водовода, L2 – длина отсасывающей
трубы. В отличие от классической
задачи колебаний жидкости в длинной трубе [45] при x = L1
< L
между напорным водоводом и отсасывающей трубой расположена турбина,
размер которой в этой постановке равен 0. Таким образом, возникает еще
одна граница, разделяющая две зоны колебаний. Первое граничное условие
на этой границе следует из постоянства расхода воды через турбину:
|
|
|
| где знаки –
и +
соответствуют
левой и правой сторонам границы разрыва. Если функция величины скачка
полного давления от объемного расхода на турбине известна, то после
линеаризации связь возмущений давления на границе разрыва можно
записать следующим образом: |
|
|
где p и q – бесконечно малые
возмущения давления и расхода, отнесенные к соответствующим параметрам
стационарного потока, p0 – невозмущенное
(размерное) давление,
соответствующее невозмущенному относительному расходу q0,
а функция
κ(q0) = 1 – f(q0) – с
точностью до постоянной суть обезразмеренная
стационарная характеристика турбины с противоположным знаком,
получаемая экспериментально. Параметры κ и χ также являются
безразмерными, член χ1 всегда больше 0 и
моделирует рассеивание энергии
в колебательном контуре. Его вычислению посвящен раздел VII этой работы.
|
Для турбины Саяно-Шушенской ГЭС, поперечное сечение канала которой S =
33.2 м2 [11], функция f(q0)
показана на рис. 1. Пока течения на
турбинах подобны, безразмерная функция κ(q0) в
соответствии с
результатами раздела V с учетом смещения точки максимума
пропорционально изменению эффективности турбины на рабочем режиме в
первом приближении должна быть применима для описания характеристик
течений в водоводах и других близких по размерам и характеристикам
турбин. При этом нормированная производная χ2(q0)
пересчитывается в
соответствии с изменением первого в правой части ее сомножителя.
Описанная здесь постановка задачи совпадает с той, что была впервые
опубликована в работах [10, 11], за исключением использования принципа
подобия, введения диссипативного члена χ1,
а также обезразмеривания и
замены некоторых обозначений. Так как величина скачка давления
соизмерима с величиной самого давления, вследствие нелинейности условий
(15) и вся задача (12) – (15) становится, строго говоря, нелинейной.
|
Решение задачи (12) – (15) для стоячих волн методом Фурье приводит к
комплексному характеристическому уравнению для комплексного волнового
вектора k (см. [10, 11]):
|
|
|
где φ – действительная часть
волнового вектора, определяющая частоту колебаний в водоводе, а ψ –
мнимая его часть, характеризующая в зависимости от знака коэффициент
затухания или возрастания колебаний. При приравнивании 0 действительной
и мнимой частей комплексного уравнения (16) получается система из двух
действительных нелинейных уравнений с двумя неизвестными φ, ψ, которая
может быть решена методом последовательных приближений. При этом
частота νe и коэффициент затухания δ (δ >
0) или коэффициент
возрастания колебаний δ (δ < 0) определяются как
|
 |
Наиболее интересным и важным с точки зрения рассматриваемых в работе
вопросов является участок стационарной характеристики турбины в зоне A’
(см. рис. 1). К сожалению, экспериментальная кривая Δp/p = f(q0)
там
слишком быстро обрывается за точкой максимума. Однако из свойств
непрерывных и гладких функций в окрестности экстремума, а также из
подобия поведения функций f(q0) и η(q0),
о чем говорилось в разделе V
этой работы, можно сделать заключение о величине функции κ(q0)
при
расходах, более существенно превышающих расход в рабочей точке турбины,
чем те, которые были первоначально показаны на рис. 1. В малой
окрестности точки максимума кривая Δp/p = f(q0),
как и любая
непрерывная и гладкая функция в окрестности этой точки, симметрична.
Это означает, что в зоне A’ производная χ(q0)
равна по модулю этой
производной в точке симметричной относительно вертикальной прямой,
проходящей через максимум зависимости Δp/p, и противоположна ей по
знаку. Поэтому оценка величины χ2 в зоне A’ при
малых отклонениях
функции κ(q0) от максимума производилась (с
точностью до знака) по ее
значениям в зоне B. При увеличении расхода q функция Δp/p = f(q0)
за
точкой перегиба вслед за функцией η(q0) в зоне
A’ (см. [12]) должна
постепенно все сильнее «заваливаться» по сравнению с Δp/p в зоне B.
Оценка этого увеличения модуля производной функция Δp/p = f(q0)
проводилась путем сравнения результатов расчета с экспериментальными
данными, что описано ниже.
|
Максимальные по модулю значения производной χ2
для стационарной
характеристики турбины, представленной на рис. 1, в окрестности точек
перегиба этой кривой, расположенных в зонах A и B соответственно
равны: χ2 = – 0.015 (κ ≈ 0.065)
и χ2 = 0.030 (κ ≈ 0.05). С учетом
вышесказанного было принято, что в зоне A’ для Саяно-Шушенской
ГЭС χ2 =
– 0.030 при κ = 0.050. В соответствии с наблюдениями амплитуда
колебаний в напорном водоводе СШ ГЭС возрастала за период в 2 раза (см.
[12, 46]). Такой же рост амплитуды колебаний из решения системы
уравнений (16) при κ = 0.050 получается, если χ = – 0.024. Отсюда
следует, что величина χ1 = 0.006.
|
| Сейсмограмма,
записанная в момент катастрофы, зафиксировала колебания
большой амплитуды на Саяно-Шушенской ГЭС с частотой 2.08 Гц [47].
Решение системы уравнений (16) только при единственной комбинации
параметров (κ = 0.275, χ = – 0.033 (χ2 = –
0.039)) одновременно приводит и к собственной частоте
колебаний νe
= 2.08 Гц и логарифмическому инкременту возрастания колебаний β = –
0.693, что означает увеличение амплитуды за период в 2.00 раза. Таким
образом, несмотря на то, что система уравнений (16) описывает
бесконечно малые колебания, при параметрах κ и χ, соответствующих
характеру изменения стационарной характеристики турбины по расходу,
решение системы (16) приводит, как можно полагать из этих
сопоставлений, к приблизительному совпадению, по крайней мере,
расчетных амплитудно-частотных характеристик процесса развития
пульсаций давления на Саяно-Шушенской ГЭС с наблюдаемыми.
|
Решение системы уравнений [16] в точке максимума на границе зон B и A’
при χ1 = 0.0060 и χ2
= 0 приводят к величине добротности θ этого
водовода равной 18.3, которая близка к добротности тромбона или
валторны [48]. Такую добротность для механического колебательного
контура можно считать высокой, что совпадает с качественными оценками,
которые дают ей специалисты в этой области [46]. Итак, принятые далее в
расчетах для Саяно-Шушенской ГЭС характерные значения функции χ = –
0.0090 в середине зоны A при κ ≈ 0.065, χ = – 0.0240 при κ ≈ 0.05 –
0.07 и χ = – 0.0320 при κ ≈ 0.25 в зоне A’ можно оценить как вполне
соответствующие наблюдавшимся при натурных испытаниях характеристикам
процессов, происходивших в водоводах ее гидроагрегатов [12]. Для других
гидроэлектростанций величины χ пересчитываются способом, указанным в
разделе VII.
|
Из результатов численных экспериментов следует, что при κ ≤ 0.30
величина параметра χ слабо влияет на частоту собственных
колебаний водовода. Максимальные
отклонения частот собственных
колебаний | Δνe |/νe
вследствие изменения величины параметра
χ, при κ ≤ 0.30 и 0 ≤ | χ | ≤ 0.025 составляют
не более 0.5 % (см. таблицу 6). Поэтому, сначала
рассмотрим частоту собственных колебаний водовода
при χ = 0 (χ2 = – χ1).
При этом k = φ, и
комплексное уравнение (16) переходит в действительное
тригонометрическое уравнение
|
|
|
Его решение также находится
методом последовательных приближений. Как показали численные
эксперименты, при многих сочетаниях параметров L1, L2
и κ для
сходимости решения первое приближение должно быть достаточно близким к
нему, так как радиус сходимости решения часто бывает мал. Поэтому, как
и в работах [10, 11] сначала был рассмотрен простейший случай
отсутствия турбины в канале,
когда κ = 1. Тогда уравнение (17) переходит в соотношение
|
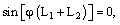 |
| имеющее очевидное решение: |
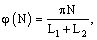 |
| где N = 1, 2, 3…, и частота
колебаний легко вычисляется: |
|
|
При κ ≈ 0.05 и L2
<< L1 результат
применения формулы (18) может
использоваться в качестве первого приближения к решению уравнения (17).
В более сложных, то есть в менее устойчивых случаях, например, при κ
> 0.1 или при κ → 0, или когда L2
~ L1, первое приближение можно
последовательно находить из предыдущих решений уравнения (17),
полученных для более устойчивого набора параметров.
|
В соответствии с указанной схемой при скорости звука c = 1350 м/с и при
χ = 0 в диапазоне изменения параметра 0 ≤ κ ≤ 0.30 был проведен
расчет первой и второй мод (N = 1, 2) собственных колебаний водовода,
длина напорной части которого L1 = 240
м, а длина отсасывающей трубы L2
= 30 м (общая длина L = 270 м). Эти параметры представляют собой
несколько округленные характеристики водовода Саяно-Шушенской ГЭС.
Частоты первой моды ν1* при этих параметрах
представлены в левой части
таблицы 6. График собственных частот этого водовода в зависимости от
величины κ показан на рис. 2 черной линией. Синяя кривая – график
второй колебательной моды. В отличие от линейного решения (см. формулу
(18)) отношение частот этих двух мод заметно превышает число 2, и в
рассмотренном диапазоне параметров изменяется от 3.0 до 2.2.
|
|
| Таблица
6 |
| N |
κ |
L1
= 240 м, L2 = 30 м |
L1
= 640 м, L2 = 30 м |
| χ
= 0 |
χ
= – 0.025 |
χ
= 0 |
χ
= – 0.025 |
| ν1*
(Гц) |
ε1
(%) |
ν2*
(Гц) |
ε2
(%) |
|
| 1 |
0.000 |
1.406 |
0 |
1.582 |
0 |
| 2 |
0.020 |
1.491 |
– 0.25 |
1.611 |
– 0.14 |
| 3 |
0.040 |
1.566 |
– 0.30 |
1.639 |
– 0.15 |
| 4 |
0.060 |
1.633 |
– 0.35 |
1.665 |
– 0.17 |
| 5 |
0.080 |
1.693 |
– 0.40 |
1.690 |
– 0.19 |
| 6 |
0.100 |
1.748 |
– 0.42 |
1.713 |
– 0.21 |
| 7 |
0.120 |
1.798 |
– 0.45 |
1.734 |
– 0.23 |
| 8 |
0.140 |
1.844 |
– 0.46 |
1.754 |
– 0.24 |
| 9 |
0.160 |
1.886 |
– 0.47 |
1.772 |
– 0.25 |
| 10 |
0.180 |
1.924 |
– 0.48 |
1.788 |
– 0.25 |
| 11 |
0.200 |
1.960 |
– 0.48 |
1.804 |
– 0.26 |
| 12 |
0.220 |
1.994 |
– 0.49 |
1.818 |
– 0.26 |
| 13 |
0.240 |
2.025 |
– 0.49 |
1.831 |
– 0.26 |
| 14 |
0.260 |
2.053 |
– 0.48 |
1.844 |
– 0.25 |
| 15 |
0.280 |
2.080 |
–
0.48 |
1.855 |
–
0.25 |
| 16 |
0.300 |
2.105 |
–
0.47 |
1.866 |
–
0.25 |
| 17 |
1.000 |
2.500 |
– |
2.015 |
– |
|
|
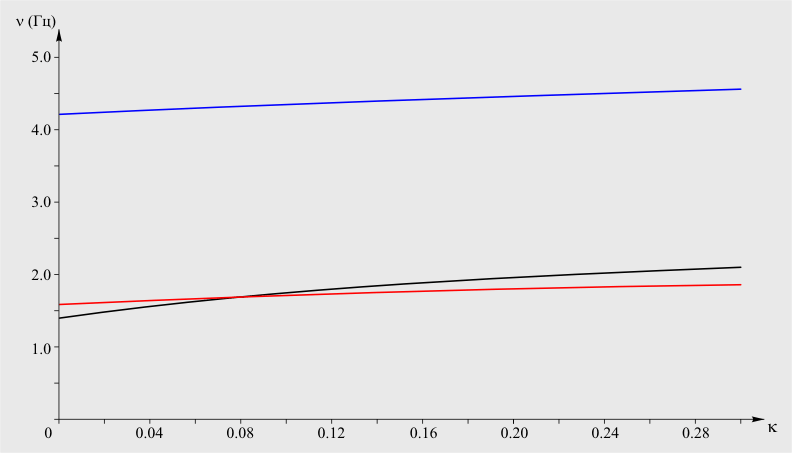 |
Рис. 2
|
|
Указанные в предыдущем абзаце параметры водовода были выбраны в
качестве стандартных для дальнейших оценок водоводов умеренной длины
(этот водовод далее называется «первым стандартным»). Собственная
частота ν1* на нижней границе κ = 0 расчетной
области по параметру κ
(идеальная турбина, на которой вся энергия потока переходит в ее
работу) была получена экстраполяцией частот при малых значениях κ. В
отсутствии турбины (κ = 1) для данного опорного водовода частоты
колебаний ν1* = 2.500 Гц и ν2*
= 5.000 Гц. Верхняя граница
рассматриваемой расчетной области κ = 0.30 была выбрана из того
условия, что при L1 = 241 м и L2
= 28 м – длинах частей напорной
системы СШ ГЭС, очень близких к длинам первого стандартного водовода,
частота и амплитуда колебаний примерно на этой границе выходят на
зафиксированные в реальности параметры больших пульсаций давления [12,
47].
|
Была рассчитана также зависимость от параметра κ частоты второй
моды ν2* водовода, длина напорной части
которого составляет 640 м, а длина
отсасывающей трубы, как и ранее, равна 30 м. Этот водовод является
стандартным для оценки характеристик водоводов большей длины, какие
бывают у тех гидроэлектростанций, у которых они не проведены по
поверхности плотины, а пробиты в горных массивах, ее окружающих.
Характеристики «второго стандартного водовода» были выбраны так, чтобы
частоты его второй моды были бы близки к частотам первой моды «первого
стандартного водовода» при наиболее важных для дальнейшего рассмотрения
значениях потерь полного давления на турбине,
соответствующих κ ≈ 0.05 – 0.10. Эти частоты ν2*
представлены
в правой части таблицы 6, а на рис. 2 график данной зависимости показан
красной кривой. Во всем рассмотренном диапазоне 0 ≤ κ ≤ 0.30 частоты
первой моды первого и второй моды второго стандартных водоводов
различаются не более чем на 13 %.
|
Частота третьей моды ν3 = 1.69 Гц
достигается на напорном водоводе
длиной L1 = 1040 м, а такая же частота
четвертой моды ν4 = 1.69 Гц –
при его длине 1440 м (при κ = 0.080). Для частоты 5.1 Гц, что может
быть близко к вихревой частоте агрегата со скоростью вращения ротора
500 об/мин, соответствующие длины напорных водоводов составят 335 м и
467 м, а для его турбинной частоты 8.33 Гц – всего 203.5 м и 284.5 м.
Так что рассмотрение третьей и четвертой мод собственных колебаний на
гидроакустический резонанс может оказаться вполне целесообразным для
высоконапорных агрегатов с большой скоростью вращения (400 – 500
об/мин), которые предполагается использовать, например, на новых
гидроаккумулирующих станциях (см. [49]).
|
Рассмотрим теперь возможность очень простой оценки собственных частот
водоводов, у которых известна только полная длина L, но неизвестны
длины обеих составляющих его частей L1
и L2. Вычислим частоту νL
|
|
|
где L* – длина соответствующего
стандартного водовода из таблицы 6, νN*
– частота его моды N = 1, 2…, L
– длина интересующего нас водовода. При постоянной длине отсасывающей
трубы L2 = 30 м изменение длины
напорного водовода L1 на ± 100 м по
сравнению с длиной стандартного водовода L1
= 240 м приводит к
максимальному отклонению оценки частоты (19) на первой моде от точного
расчета ν1 не более чем
на 3.4 %, см. таблицу 7.
|
|
| Таблица
7 |
| N |
L1 (м) |
L2 (м) |
κ |
ν1 (Гц) |
νL
(Гц) |
νL/ν1 |
|
| 1 |
140 |
30 |
0.040 |
2.574 |
2.487 |
0.966 |
| 2 |
240 |
30 |
0.040 |
1.566 |
1.566 |
1.000 |
| 3 |
340 |
30 |
0.040 |
1.146 |
1.143 |
0.997 |
|
|
| 4 |
140 |
30 |
0.080 |
2.715 |
2.689 |
0.990 |
| 5 |
240 |
30 |
0.080 |
1.693 |
1.693 |
1.000 |
| 6 |
340 |
30 |
0.080 |
1.260 |
1.235 |
0.980 |
|
|
| 7 |
140 |
30 |
0.200 |
3.048 |
3.113 |
1.021 |
| 8 |
240 |
30 |
0.200 |
1.960 |
1.960 |
1.000 |
| 9 |
340 |
30 |
0.200 |
1.475 |
1.430 |
0.969 |
|
|
Изменение длины отсасывающей
трубы вдвое от номинала L2 = 30 м до 15
м или до 60 м вызывает
отклонения от точного значения частоты ν1
не более чем на 5.2 %, см.
таблицу 8. Так как на второй моде частота по параметру κ изменяется
меньше, чем на первой, указанный здесь метод пересчета частот по полной
длине водовода даст в этом случае еще меньшую погрешность.
|
|
| Таблица
8 |
| N |
L1 (м) |
L2 (м) |
κ |
ν1 (Гц) |
νL (Гц) |
νL/ν1 |
|
| 1 |
240 |
15 |
0.040 |
1.697 |
1.658 |
0.977 |
| 2 |
240 |
30 |
0.040 |
1.566 |
1.566 |
1.000 |
| 3 |
240 |
60 |
0.040 |
1.487 |
1.409 |
0.948 |
|
|
| 4 |
240 |
15 |
0.080 |
1.892 |
1.793 |
0.948 |
| 5 |
240 |
30 |
0.080 |
1.693 |
1.693 |
1.000 |
| 6 |
240 |
60 |
0.080 |
1.559 |
1.524 |
0.978 |
|
|
| 7 |
240 |
15 |
0.200 |
2.191 |
2.075 |
0.947 |
| 8 |
240 |
30 |
0.200 |
1.960 |
1.960 |
1.000 |
| 9 |
240 |
60 |
0.200 |
1.732 |
1.764 |
1.018 |
|
|
Таким образом, в рассматриваемом диапазоне параметров совместное
влияние всех отклонений решения по соотношению (19) при использовании
таблицы 6 от точного решения нелинейной системы уравнений (16) не
превышает ~ 6 %. Такой точности вполне достаточно для первичных оценок
частот собственных колебаний напорных водоводов интересующих нас
гидроэлектростанций. Однако, при таком подходе не определяются
коэффициенты затухания колебаний, имеющие, как показано далее,
критически важное значении для определения степени опасности развития
катастрофических последствий возможного резонанса. Поэтому оценки
описанным выше приближенным методом могут служить только для принятия
предварительного решения о том, нужно или нет более углубленное
изучение характеристик напорной системы, и отказываться от него можно
только в совершенно очевидных случаях, примеры которых будут
продемонстрированы далее в разделе IX.
|
|
VII – Определение коэффициента
затухания колебаний в точке максимума расходной характеристики турбины
для произвольной напорной системы
|
Как показали дальнейшие исследования, для анализа устойчивости напорных
систем необходимо достаточно точно знать коэффициент затухания δ = δ1
при отсутствии нелинейной обратной связи в колебательной системе, то
есть при χ = χ1 (в этом
случае χ2 = 0). Эта точка соответствует
максимуму расходной характеристики турбины. Для Саяно-Шушенской ГЭС
параметр χ1 = 0.0060 был определен в
предыдущем разделе работы из
сопоставления расчетных и экспериментальных данных. В результате
решения системы уравнений (16) при этом значении χ1
определяется
значение коэффициента затухания δ1.
Необходимо построить метод
пересчета этого параметра с характеристик СШ ГЭС на характеристики,
соответствующие другим рассматриваемым объектам.
|
Исследуемое здесь естественное затухание колебаний вызывается двумя
основными причинами: диссипацией энергии колебаний в водоводе и
излучением энергии через его открытые концы. Так как характерная длина
волны на 2 порядка больше, чем диаметр водовода, на процесс излучения
не влияют всякие локальные особенности, связанные с малыми изменениями
геометрии водовода, формой его элементов, структурой его поверхности и
тому подобному. Определив потери энергии на излучение и зная общие
потери в водоводе СШ ГЭС, можно оценить там диссипативные потери.
Затем, используя связь между
ними и перепадом давления на турбине, пересчитать диссипативные потери,
получив, таким образом, полные потери, и, соответственно, коэффициент
затухания δ1 для водовода любой
рассматриваемой далее напорной
гидроэлектростанции.
|
Из аддитивности коэффициента затухания
|
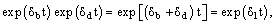 |
| следует, что |
|
|
| где δb
– часть коэффициента
затухания δ1, определяемая
излучением, δd – часть, вызываемая
диссипацией. |
|
Потери на излучение зависят от частоты колебаний, которая, в принципе,
сама зависит от этих потерь. Однако в предыдущем разделе работы было
показано, что параметр χ, ответственный в системе уравнений (16) за
затухание или возрастание колебаний, в интересующем нас диапазоне
величин очень слабо влияет на их частоту, а, значит, и на форму
собственной функции стоячей волны. Поэтому, для оценки потерь на
излучение можно выбрать расчетный случай при χ = 0, и, таким образом,
свести систему уравнений (16) к единственному уравнению (17) только для
действительной части волнового вектора φ. |
|
Рассчитаем при этих условиях потери на излучение из трехмерного
осесимметричного канала постоянного сечения (трубы) с двумя открытыми
концами, диаметр которого мал по сравнению с его длиной, но не равен 0,
как было принято в математической модели, базирующейся на системе
уравнений (12) – (15). В этом канале возникает стоячая волна,
характеристики которой можно вычислить, используя известные результаты,
приводимые в учебниках по акустике (см., например, [45]). Правда, эти
вычисления относятся к классическому решению волнового уравнения без
дополнительной внутренней границы раздела. Однако, сравнивая формы
собственных функций решений системы уравнений (12) – (15) с решениями
классической задачи, можно этой разрывной задаче поставить в
соответствие эквивалентную по характеристикам излучения классическую
задачу. |
|
На рис. 3 показаны модельные примеры собственных решений задачи (16).
При χ = 0 амплитуда колебаний давления получается в следующем виде: |
|
|
где pm –
максимальная амплитуда
колебаний. Так как κ ~ 0.05, амплитуда колебаний в отсасывающей трубе
при x > L1 на порядок и более
ниже, чем в напорном водоводе при
x < L1.
|
На рис. 3 (a) изображена собственная функция первой моды колебаний
(сплошная черная линия) с разрывом, отображающим перепад амплитуды на
турбине, для случая, когда длина отсасывающей трубы (участок решения
справа от разрыва) существенно меньше длины напорного водовода. В
принципе, можно представить и обратную ситуацию, когда длины этих двух
частей канала находятся в обратной пропорции (см. рис. 3 (b)). Такое
тоже бывает на некоторых гидроэлектростанциях. На рис. 3 (c) показана
собственная функция второй моды стоячей волны снова для водовода с
короткой отсасывающей трубой. Синим пунктиром изображены продолжения
собственных функций соответствующих мод классической (безразрывной)
стоячей волны в напорном водоводе, имеющей ту же частоту колебаний, что
и волна, получаемая из решения задачи с разрывом. Красный пунктир – то
же самое для стоячей волны в отсасывающей трубе. Видно, что влияние
разрыва (турбины) на собственную функцию в вариантах стандартного
размещения турбины (a) и (c) при короткой отсасывающей трубе сводится к
«выеданию» части собственной функции для напорного водовода некоторой
иной («эквивалентной») длины, и «пристыковке» к ней части собственной
функции для отсасывающей трубы. При этом последняя также рассчитывается
для классической трубы без разрыва в наполняющей ее среде, и длина ее
равна длине эквивалентной трубы. Это приводит к уменьшению длины
стоячей волны по сравнению с ее безразрывным вариантом, и,
соответственно, длины канала, в котором она может реализоваться с
данной частотой. В варианте (b), напротив, длина водовода несколько
увеличивается по сравнению с трубой без разрыва, в которой существует
стоячая волна той же частоты.
|
|
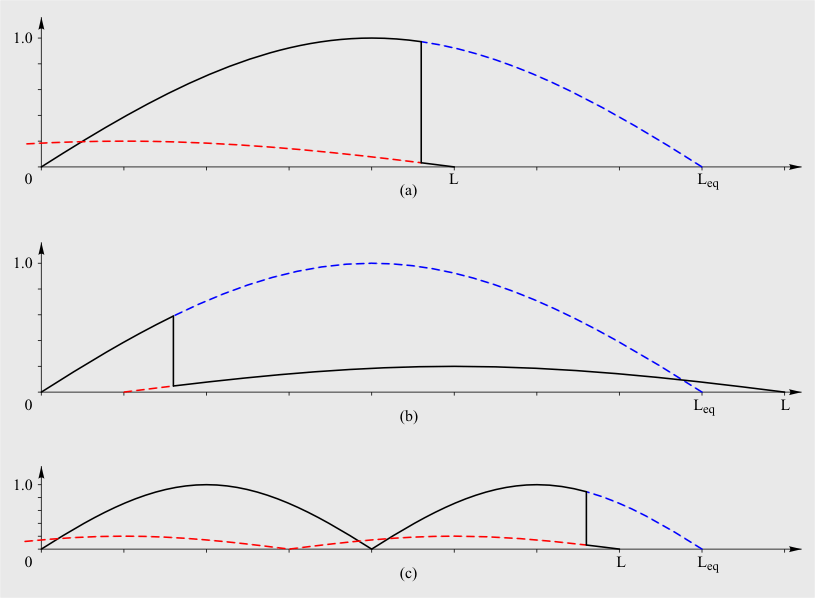 |
Рис. 3
|
|
Длина канала, в котором неразрывная собственная функция стоячей волны
соответствует той же частоте, что и разрывная, выше была названа
эквивалентной. Очевидно, что эквивалентная длина Leq
вычисляется
следующим образом:
|
|
|
где c – скорость звука, N – номер
моды, νe –
собственная частота волны, полученная из разрывного решения уравнения
(17).
|
|
Известно, что сдвиг узла ΔL от открытого конца канала постоянного
сечения (трубы) вследствие конечности его (ее) диаметра (то есть
изменение длины стоячей волны) оценивается как |
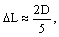 |
| где D – диаметр трубы (см.
[45]). Это означает, что узлы давления, которые в случае одномерного
решения волнового уравнения (для бесконечно тонкой трубы) находились
точно на ее концах (см. граничное условие (13)), смещаются внутрь
трубы, и ее концы становятся источниками возмущения окружающей среды,
вызывая излучение энергии стоячей волны в окружающее пространство и
постепенное затухание этой волны [45]. |
|
Амплитуда колебаний давления на торце напорного водовода оказывается
равной |
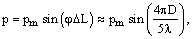 |
где – φ действительная часть волнового вектора,
λ – длина волны, pm – максимальная
амплитуда колебаний. При D
<< λ
|
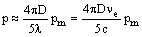 |
| На конце отсасывающей трубы
амплитуда колебаний будет в κ–1 (то
есть в 10 – 20) раз меньше. |
|
Тогда средняя плотность потока энергии q на срезе напорного водовода
составит величину (см. [45]) |
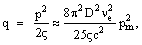 |
| где ς = ρc
– удельное акустическое сопротивление. Убыль энергии – ΔE за период с
открытого отверстия будет равна |
|
|
| где Sb –
площадь поверхности
излучения c одного конца трубы. При этом полная энергия колебаний в
водоводе эквивалентной длины Leq равна |
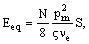 |
| где N – номер моды, S – площадь
поперечного сечения излучающей трубы (см. [45]). |
|
Если бы диаметр водовода был бы строго постоянен по всей длине, тогда
бы Sb = S. Однако, для плавного входа
потока воды в напорный водовод
его входное отверстие делают заметно больше его внутреннего диаметра.
Еще более сложную форму имеет отсасывающая труба, выходное отверстие
которой, по крайней мере, на порядок больше, чем сечение канала за
турбиной. Таким образом, с акустической точки зрения части водовода
выполнены в виде своеобразных раструбов с заметным увеличением площади
выходных отверстий, которую и надо брать в качестве параметра Sb
в
формуле (23). Это обстоятельство удобно выразить следующим образом: |
|
|
| где kb –
коэффициент отношения
площади излучения к площади поперечного сечения водовода. Рассмотрение
имеющихся чертежей водоводов Саяно-Шушенской и Чиркейской ГЭС [50, 51]
показывает, что для их напорных водоводов коэффициент kb
приблизительно
равен 2.6 и 3.4 соответственно. Для других рассматриваемых далее
гидроэлектростанций, у которых водоводы турбин открыты в водохранилище,
принято, что среднее значение этого параметра равно 3.0. Для
отсасывающих труб kb ≈ 10. |
|
Отношение полной энергии водовода реальной длины и этого же параметра
водовода эквивалентной длины равно отношению интегралов |
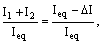 |
где I1 – интеграл от
собственной функции по
интервалу L1 (по длине напорного
водовода), I2 – по интервалу L2
(по
длине отсасывающей трубы), Ieq –
интеграл по эквивалентной длине, ΔI –
по «выеденной» разрывом части собственной функции (см. рис. 3 (а) и 3
(c)).
|
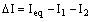 |
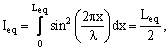 |
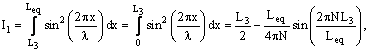 |
| где L3
= Leq – L1.
Величиной
интеграла I2 по отсасывающей трубе
можно пренебречь, так как при |
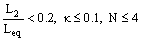 |
| его отношение к Ieq
составляет
не более 0.8 %: |
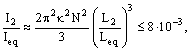 |
|
Тогда |
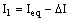 |
| Поэтому полная энергия
колебаний в водоводе для типичной «короткой» (L2
< 0.2 Leq)
отсасывающей трубы может быть вычислена следующим образом: |
|
|
|
Отношение потерь энергии за период к запасенной в колебательном контуре
ее величине равно логарифмическому декременту затухания β (при β
<< 1) (см., например, [45]). Поэтому из формул (22) –
(25) следует, что часть декремента затухания, за которую ответственно
акустическое излучение из открытого конца напорного водовода, составит |
|
|
| Для отсасывающей трубы правую
часть формулы (26) вследствие снижения там амплитуды колебаний
в κ–1
раз надо умножить на k2, что даст
уменьшение вычисляемой величины в 100
– 400 раз. Поэтому даже увеличение коэффициента kb
примерно в 3 раза
приведет к тому, что этот часть декремента затухания составит не более
чем 3 % от того, что дает напорный водовод. Следовательно, акустическим
излучением из отсасывающей трубы можно пренебречь, и формула (26) для
напорного водовода дает практически полную оценку соответствующей части
декремента затухания βb. Тогда часть
коэффициента затухания, вызванная
акустическим излучением равна |
|
|
|
Таким образом, для определения потерь на акустическое излучение из всех
конструктивных параметров отсасывающей трубы достаточно знать только ее
длину L2. У напорного водовода должны
быть известны его длина L1,
диаметр D и степень его уширения на входе kb.
Впрочем, последний
параметр вполне можно оценить на основе корреляции с известными
величинами или, в некоторых нестандартных случаях, опираясь на здравый
смысл. |
|
Перейдем теперь к рассмотрению диссипативных потерь. Ими в слабо
изогнутом гладком водоводе практически постоянного сечения без разрывов
среды можно полностью пренебречь [52]. Диссипативные потери в
отсасывающей трубе, имеющей более сложную форму, пренебрежимо малы
из-за малой интенсивности там амплитуды колебаний. Поэтому единственным
значимым источником потерь могут быть только турбина и ее «обвязка». В
этом месте в водоводе изменяется поперечное сечение, канал
закручивается, а затем «ломается». При этом даже те волны, длины
которых близки к длине водовода, могут терять там некоторую часть
собственной энергии. |
|
В рассматриваемой модели стоячей волны все это сводится к потерям на
скачке акустического давления в точке, где расположена турбина. Как
известно, в гидродинамике практически всегда эти потери считаются
пропорциональными перепадам давления [14]. Так как акустическое
давление p везде в уравнениях является безразмерным, его необходимо
умножить на параметр, с помощью которого оно было обезразмерено. Тогда |
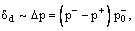 |
| где p–
и p+ – безразмерные
акустические давления до и после разрыва решения. Из решения (21) (см.
также рис. 3 (a) и 3 (c)) следует, что |
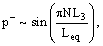 |
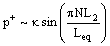 |
| Давление перед турбиной p0–
равно |
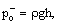 |
| где h – напор воды. Так как ρ,
g = const |
|
|
| и |
|
|
где символом * обозначены
параметры Саяно-Шушенской ГЭС. Тогда при известном значении δ1*
= 0.267
(полученном из решения системы уравнений (16) при κ = 0.035 и χ1
=
0.0060) с помощью соотношений (20), (26) и (27) определяется
коэффициент затухания δd*, а затем из (26) –
(29) и (20) вычисляется
значение коэффициента затухания δ1 для
любой высоконапорной
гидроэлектростанции. Далее, решая систему уравнений (16) в
точке χ2 =
0, можно вычислить параметр χ1 для
данной напорной системы и
использовать его для расчетов в любой другой точке обезразмеренной
стационарной характеристики турбины этой гидроэлектростанции.
|
|
VIII – Известные инциденты на
гидроэлектростанциях, связанные с гидроакустическим резонансом
|
Теперь, опираясь на результаты разделов VI – VII, будем получать и
исследовать полные решения системы уравнений (16) для различных
напорных систем. Подробное описание техники решения системы (16)
выходит за рамки излагаемой задачи, и, поэтому, здесь не приводится.
Вместо этого разберем инциденты на гидроэлектростанциях, связанные с
гидроакустическим резонансом и генерированием автоколебаний в напорном
водоводе, выявленные к настоящему моменту. Один из них широко известен
– это катастрофа на Саяно-Шушенской ГЭС. Несмотря на ее уникальность, в
последние месяцы периодически проскальзывали мнения (впрочем,
подтверждаемые лишь тем, что в обоих случаях по непонятной причине
отрывалась турбинная крышка), что имеются некоторые аналогии между этой
катастрофой и аварией, произошедшей 9 июля 1983 года на Нурекской ГЭС
(см., например, [20]).
|
|
Как доказано в работе [3], вылет второго гидроагрегата Саяно-Шушенской
ГЭС произошел из-за глобальной потери устойчивости течения в напорном
водоводе этого агрегата вследствие возникновения в нем условий для
генерирования быстро возрастающих колебаний давления. Подобные
автоколебания хорошо известны, например, в радиотехнике с начала XX
века. Одним из первых генераторов таких электромагнитных колебаний
является еще ламповый автогенератор Ван-дер-Поля (см., например, [53]).
В настоящее время имеются различные автогенераторы электромагнитных
колебаний на твердотельных элементах. Впрочем, механические
автогенераторы колебаний – часы-ходики известны уже не одну сотню лет.
Тем не менее, применение подобных принципов для рассмотрения процессов
в водоводах гидроэлектростанций, кажется, до сих пор еще не стало
привычным в гидроэнергетике. |
|
Для возникновения и развития автоколебаний в генераторе кроме
колебательного контура должен быть еще один обязательный нелинейный
элемент, при наличии которого и возникает положительная обратная связь,
вызывающая рост инициированных в контуре колебаний до тех пор, пока
вследствие нелинейности всех элементов генератора потери в контуре за
период колебаний не станут равными той энергии, которая вносится в
контур за счет обратной связи [53]. Вследствие того, что задача (12) –
(15) сформулирована для акустических (бесконечно малых) колебаний,
решая ее, невозможно определить пределы роста возмущений в водоводе.
Однако натурный опыт ценой в 75 человеческих жизней – отрыв крышки
второго гидроагрегата Саяно-Шушенской ГЭС и его вылет приблизительно на
14 м вверх [3] доказывает, что эти пределы находятся далеко за теми
уровнями давления воды, которые можно допускать при эксплуатации ГЭС. |
|
Нелинейным элементом, создающим положительную обратную связь в
генераторе пульсаций давления, возникающих в водоводе, как следует из
предыдущего рассмотрения, является радиально-осевая турбина.
Автогенерация колебаний возникает тогда, когда знак функции χ из
системы уравнений (12) – (15) или (16) отрицателен. Это имеет место
быть в зонах A и A’ (см. рис. 1), то есть в левой части области не
рекомендуемой работы II и в области запрещенной работы IV. |
Результаты расчетов системы уравнений (16) при указанных в предыдущем
разделе значениях параметров κ и χ для водовода Саяно-Шушенской ГЭС
показаны в таблице 9. Частота колебаний водовода νe
в точке максимума
на границе зон B и A’ – минимальное значение частоты собственных
колебаний этой системы, оказалась равна 1.55 Гц, что всего на 0.10 –
0.15 Гц выше частоты колебаний вихревого возбуждения νv,
составляющей
1.40 – 1.45 Гц (различия не превышают 6 – 10 %). При уходе
колебательной системы на более-менее прямолинейный участок функции κ,
частота ее колебаний вырастает до 1.60 Гц, а логарифмический инкремент
возрастания β = δ/νe становится равным – 0.672.
Следовательно,
амплитуда колебаний давления за период увеличивается в 1.96 раза. Из-за
«заваливания» функции χ(q0)
по q0 в зоне A’, при κ = 0.275 значение
функции χ = – 0.033. Тогда при частоте осцилляций давления большой
амплитуды νe = 2.08 Гц [12, 47], как
уже упоминалось в разделе VI, инкремент возрастания β = – 0.693, что
соответствует двукратному росту амплитуды колебаний за период.
|
|
Выбор параметров в этих расчетах опирался на не вполне строгие с
математической точки зрения основания, но сравнение представленных в
таблице 9 данных с характеристиками явлений, наблюдавшихся при натурных
испытаниях гидроагрегатов СШ ГЭС и при развитии катастрофы, а также с
результатами гидродинамических оценок сил, воздействовавших на
турбинную крышку второго гидроагрегата [3], указывает на полную
адекватность этих расчетов. Верхняя строчка из части таблицы,
относящейся к СШ ГЭС, выделена жирным шрифтом, так как именно эти
параметры, как показано в разделе X, являются ключевыми для возбуждения
неограниченно растущих (в интересующих нас временах и масштабах)
автоколебаний. Для запуска автоколебаний необходима близость частоты
внешнего возбуждения (1.40 – 1.45 Гц) и собственных частот (1.55 Гц).
После того, как автоколебания запущены, внешнее возбуждение перестает
влиять на этот процесс, и уход частоты автоколебаний от частоты
возбуждения уже не играет никакой роли в его дальнейшем развитии [53]. |
|
Попадание второго гидроагрегата СШ ГЭС при его остановке в зону A’ 17
августа 2009 года в 8:13 при напоре 212 м [5], близком к максимальному,
произошло вследствие быстрого полного открытия лопаток направляющего
аппарата, вызванного, по-видимому, сбоем или отказом системы управления
лопатками направляющего аппарата. Описанный сценарий полностью
объясняет все явления, происходившие со вторым гидроагрегатом в момент
катастрофы (см. [3]). |
|
| Таблица
9 |
| ГЭС |
L1 (м) |
L2 (м) |
κ |
νe
(Гц) |
β |
νv
(Гц) |
σ |
|
| СШ |
241 |
28 |
0.035 |
1.55 |
0.172 |
1.425 ± 0.025 |
0.60 ± 0.12 |
| 0.050 |
1.60 |
– 0.672 |
| 0.275 |
2.08 |
– 0.693 |
|
|
| Нурекская |
649 |
34.5 |
0.080 |
0.720 |
0.281 |
0.63 ± 0.07 |
0.55 ± 0.45 |
| 0.0875 |
0.730 |
– 0.546 |
| 0.095 |
0.743 |
0.272 |
| 666 |
34.5 |
0.080 |
0.705 |
0.285 |
0.50
± 0.45 |
|
|
|
Авария первого гидроагрегата на Нурекской ГЭС, случившаяся 9 июля 1983
года в 22:48, через 4 минуты после его включения в сеть, произошла на
мощности 220 МВт и при напоре 203 м, что на 3 м ниже минимально
допустимого напора [20]. В таблицах 1, 3 и 5 именно этот режим был
назван «Нурекская ГЭС - 2». По оценке расход воды на этом режиме с
учетом снижения эффективности η до 0.89 составляет 126.5 м3/с,
так что
q = 0.74. Граница раздела зон A и B находится, примерно, при q = 0.68
(именно там при отсутствии автоколебаний возникают самые большие
пульсации давления из всей области не рекомендованных режимов работы
турбины, и, соответственно, самые большие вибрации гидроагрегата (см.
[10 – 12])). Различие между этими двумя точками невелико. Кроме того, в
условиях больших пульсаций давления возникают колебания мощности на
шинах электрогенератора, которые могут составлять не менее 10 % от
среднего значения, см. [12]. Тогда номинальная мощность гидроагрегата
на этом режиме могла быть около 200 МВт. В этом случае оценка
«стационарного» расхода воды без учета его пульсаций снижается до 118 м3/с, и q = 0.69 (режим Нурекская ГЭС - 3), что практически совпадает с
точкой минимума на стационарной характеристике (построенной, заметим,
по данным, полученным на агрегате Саяно-Шушенской ГЭС). |
|
Отметим, что различие параметров подобия ζ для режимов Нурекская
ГЭС –
2, 3 и СШ ГЭС – 3, который также соответствует этой же точке
минимума
на стационарной характеристике, составляет всего 1 – 4 % (см. таблицу
5). Таким образом, пересчет параметров на основе теории подобия в
данной ситуации вполне обоснован. Следовательно, можно утверждать, что
развитые в разделах III – VII этой работы методы должны давать
правильные результаты при анализе аварии на Нурекской ГЭС. |
|
Из оценок следует, что она произошла при выводе первого гидроагрегата
на рабочий режим в момент достижения окрестности максимума потерь
полного давления, и, следовательно, в момент, когда интенсивность вихря
за турбиной оказалась максимальной на всем интервале расходов от 0 до
рабочей точки (см., например, [12]). При этом производная χ2
= 0, а
суммарное значение χ положительно, и режим генерирования автоколебаний
возникнуть здесь не может. Однако, за несколько секунд до этого на
падающем участке функции Δp/p собственная частота колебаний на первой
моде равна там 0.73 Гц (см. таблицу 9), а вихревая частота на режиме B
оценивается в 0.56 – 0.70 Гц (различия составляют 4 – 23 %). Скорость
роста колебаний на этом режиме составляла 73 % (β = – 0.546 дает
возрастание амплитуды в 1.73 раза за период) от того, что было на
режиме генерирования колебаний в момент катастрофического роста
пульсаций давления на СШ ГЭС. Но здесь, на Нурекской ГЭС, режим
генерирования быстро и самопроизвольно прекратился после 2 – 3
пульсаций перед выходом в точку минимума кривой Δp/p, где χ снова
оказалось больше 0. Таким образом, быстрый всплеск пульсаций давления,
достигнув максимальных значений в окрестности точки экстремума, также
быстро прекратил свой рост. Данное обстоятельство принципиально
отличает этот процесс от того, что происходило в момент катастрофы на
СШ ГЭС во время глобальной потери устойчивости потока воды в водоводе
(следует сравнить последние строчки таблицы 9 в разделах СШ ГЭС и
Нурекская ГЭС при L1 = 649 м). |
|
В течение короткого периода существования интенсивных пульсаций
давления гидродинамические силы, действующие на турбинную крышку,
превышали величину проектного затяга ее шпилек. В этом случае сила
трения уже не препятствует боковым перемещениям крышки под действием
разнообразных циклических сил, вызванных, например, неполной
сбалансированностью ротора гидроагрегата. Единственным препятствием для
таких перемещений крышки становятся сами шпильки, работающие на срез,
что приводит к быстрому образованию в них усталостных трещин, резко
снижающих растягивающую нагрузку, которую они способны нести. При этом
трещины сами начинают расти под действием этих нагрузок, и при
неоднократных повторениях такого режима рано или поздно шпильки
разрушаются (см. [3]). Подобные явления при данном напоре могли
происходить неоднократно при прохождении зон A и B. В конце концов,
разрушилось критическое число шпилек, и после этого процесс их
усталостного разрушения при последнем проходе зоны A пошел
лавинообразно. Но тут агрегат вышел из зоны A, что сопровождалось
прекращением роста пульсаций давления и гидродинамических нагрузок на
турбинную крышку и даже их снижением. |
|
Оборвалось только 50 шпилек из 72 [20], крышку приподняло, через
образовавшуюся щель потекла вода, и гидроакустические характеристики
водовода изменились. Сила давления на крышку еще более снизилась, и она
«зависла» в полуоторванном положении. Через 6 минут агрегат был
отключен, еще через 4 минуты он был остановлен, а через 38 минут для
предотвращения затопления машинного зала были опущены затворы нижнего
бьефа [20]. Таким образом, вследствие самопроизвольного затухания
автоколебаний, возникших в зоне A (при расходах меньших, чем расход на
рабочем режиме), авария первого гидроагрегата Нурекской ГЭС не
переросла в катастрофу. Напротив, на Саяно-Шушенской ГЭС автоколебания
возникли при расходах, бóльших, чем расход на рабочем режиме (в зоне
A’), и никаких сдерживающих их развитие факторов вплоть до вылета
агрегата из турбинного колодца не было. Пульсации давления непрерывно и
интенсивно (примерно вдвое за период) возрастали, турбинная крышка, в
конце концов, была оторвана осевой силой, превышающей силу прямого
разрыва ее шпилек, и второй гидроагрегат СШ ГЭС был выброшен в машинный
зал. Из открытого турбинного колодца туда хлынул мощный поток воды,
который разрушил в машинном зале почти все и погубил 75 человек [3].
Низкая прочность шпилек крепления крышки второго гидроагрегата в момент
ее отрыва только ограничила максимальный уровень давления на пике
колебаний, снизив тем самым возможный уровень разрушений при
катастрофе. Более того, эта прочность непрерывно падала непосредственно
в процессе возрастания пульсаций давления вследствие быстрого роста
трещин в шпильках. |
|
Таким образом, процессы, которые привели к рассмотренным инцидентам на
Саяно-Шушенской и Нурекской ГЭС были совершенно одинаковыми – в обоих
случаях произошло генерирование автоколебаний в гидроакустических
колебательных напорных системах. Однако происходили они в разных
условиях – в зоне A стационарной характеристики турбины Нурекской ГЭС и
в зоне A’ турбины ГЭС Саяно-Шушенской. Именно вследствие различия этих
«граничных условий» столь различным оказался и конечный результат.
Можно также отметить, что первый из инцидентов произошел при напоре,
который был ниже нижнего допустимого уровня, а второй – в окрестности
его верхнего уровня. Очевидно, что при удалении в любую сторону от
оптимальной рабочей точки возмущения со стороны затурбинного вихря
растут, в конце концов, превышая пределы естественной устойчивости
агрегата, которую обеспечивает диссипативный коэффициент χ1
> 0,
а также различия в собственных частотах колебаний и частотах
возбуждения. Более подробно этот вопрос будет рассмотрен в разделе X
данной работы. |
|
В последней строке таблицы 9 показаны характеристики напорной системы в
точке максимума (по модулю) наклона стационарной характеристики турбины
в зоне A с третьим, самым длинным водоводом Нурекской ГЭС, имеющим
самую низкую частоту собственных колебаний. Увеличение длины водовода
чуть приблизило собственную частоту колебаний к вихревой, однако,
естественный разброс вихревых частот, который наблюдается на разных
агрегатах даже одной и той же гидроэлектростанции (см. [11, 12]),
существенно превышает это малое сближение частот. Кроме того, в момент
аварии все агрегаты, кроме первого находились на рабочем режиме, и они
могли выйти на него при несколько большем уровне напора воды, быть
может, даже не бывшим в то время за допустимыми границами. Именно
поэтому в аварию попал первый, а не третий или второй агрегаты
Нурекской ГЭС, устойчивость на возникновение автоколебаний у которых в
зоне A формально чуть ниже, чем у первого (см. последний столбец
таблицы 9; приведенные в нем данные подробно описаны в разделе X). |
|
IX – Пример первичного отбора
гидроэлектростанций в группу риска
|
|
Воистину, не зря сказано: издалека многое кажется непонятным и
невозможным, но при ближайшем рассмотрении оказывается простым и
естественным. |
|
В. Звягинцев |
|
|
Применим теперь разработанную полуэмпирическую теорию к группе уже
рассмотренных в предыдущих разделах гидроэлектростанций. При этом
сначала используем самый простой метод оценки собственных частот
напорных водоводов с помощью пересчета частоты колебаний стандартных
водоводов для гидроэлектростанций умеренной напорности, а также для ГЭС
Гувер. У Красноярской ГЭС, Итайпу и Санься водоводы расположены по
внешней относительно водохранилища стороне плотины. Известны
минимальные напоры для этих станций, а это и есть высоты их напорных
водоводов. Вследствие примерного геометрического подобия пересчетом с
данных Саяно-Шушенской и Чиркейской ГЭС (там из-за шахматного
расположения гидроагрегатов следует брать длину короткого напорного
водовода) легко получить оценки длин этих водоводов. Длины отсасывающих
труб были приняты равными 30 м, что должно быть близко к типичному их
значению для таких конструкций плотин. Длина водоводов гидростанции
Гувер определялась по схеме из ссылки [22]. Таким образом были получены
оценки полных длин водоводов этих станций, см. таблицу 10. |
|
Из того, что
уровни эффективности турбин этих станций на номинальном рабочем режиме
близки к 0.9, следует, что минимальные потери полного давления
находятся на уровне κ ≈ 0.10. В соответствии с этим для оценки частот
собственных колебаний всех этих станций из таблицы 6 была взята частота
первой моды первого стандартного водовода νe*
= 1.75 Гц (см. таблицу
6). После пересчета на длины их водоводов со стандартной по формуле
(19) были получены частоты νe,
представленные в соответствующем столбце
таблицы 10. |
|
Пересчет по
формуле (8) вихревой частоты Красноярской ГЭС, как наиболее близкой по
параметру оптимальности типа турбины ξ (50 < ξ < 70) к
ГЭС Итайпу
и Санься, дает для них значения частоты νv
из предпоследнего столбца
таблицы 10. Для ГЭС Гувер эта частота пересчитывалась по
соответствующей частоте СШ ГЭС, так как обе они относятся к подобласти
30 < ξ < 50 параметра оптимальности ξ. |
|
| Таблица
10 |
| ГЭС |
L
(м) |
κ |
νe
(Гц) |
νv
(Гц) |
νr
(Гц) |
|
| Гувер |
145 |
0.10 |
3.3 |
1.8 |
3.00 |
| 130 |
3.6 |
| Красноярская |
135 |
0.10 |
3.5 |
1.2 |
1.56 |
| Итайпу |
125 |
3.8 |
1.2 |
1.53 |
| Санься |
115 |
4.1 |
1.0 |
1.25 |
|
|
|
Сравнивая частоты
собственных колебаний водоводов νe и
вихревые частоты νv у
рассматриваемых 4 гидроэлектростанций, можно наглядно убедиться, что
вследствие большого различия частот опасности возникновения
автоколебаний в напорных водоводах, возбуждаемых затурбинным вихрем,
нет. Однако имеется еще один источник сильных возмущений – сама
турбина. Пульсации давления с частотой вращения турбины могут быть, как
минимум, не менее интенсивными, чем с вихревой частотой. То, что в
качестве частоты возбуждения ранее рассматривалась только вихревая
частота νv, вызвано только тем, что в
обоих инцидентах с
автоколебаниями в водоводе резонанса на турбинной частоте, очевидно, не
было. Теперь в последнем столбце таблицы 10 показаны и турбинные
частоты. В случае гидроэлектростанций умеренной напорности в принципе
ничего не меняется – различие между собственными частотами и частотами
возбуждения остается слишком большим. Поэтому в данной ситуации не
требуется более подробное и глубокое изучение устойчивости работы этих
станций. Ясно – они устойчивы. |
|
Легко понять, что
это относится и ко всем другим средне- и низконапорным
гидроэлектростанциям с водоводами, расположенными на поверхности
плотины, так как и турбинные и вихревые частоты у них низки вследствие
достаточно малой частоты вращения их турбин (чем ниже напор, тем
медленнее вращаются радиально-осевые турбины), а частоты собственных
колебаний водоводов, наоборот, высоки из-за их малой длины. Если же
длина водоводов не коррелирует напрямую с напором, как у довольно
многих «горных» ГЭС или гидроаккумулирующих станций, то оценка их
гидроакустической устойчивости может оказаться совсем иной даже при
сравнительно низких напорах. |
|
Как уже отмечалось ранее, высшие гармоники возбуждающих колебаний здесь
не рассматриваются вследствие их существенно более низких амплитуд. Для
ГЭС с другими типами турбин нужно строить и другую теорию устойчивости,
если она вообще для них нужна, что не является самоочевидным. Ведь
известно, что турбины с поворотными лопастями работают на любых
переходных режимах существенно лучше, чем радиально-осевые агрегаты с
неизменной геометрией лопастей. А на очень высоконапорных
гидроэлектростанциях с ковшовыми турбинами, кажется, до сих пор еще не
зафиксировано возникновения опасных автоколебаний в напорных водоводах,
хотя это может быть и связано только с ограничениями в доступе к
подобной информации. |
|
У высоконапорной гидростанции Гувер собственные частоты длинного
водовода оказались в опасной близости к турбинным частотам. Отношение |
Δν |/νe < 0.1 примерно как у
Саяно-Шушенской и Нурекской ГЭС.
Поэтому эту гидроэлектростанцию следует отнести к группе риска и
получить более точные оценки ее гидроакустической устойчивости. |
|
X – Получение критерия
возбуждения автоколебаний и оценка гидроакустической устойчивости
высоконапорных гидроэлектростанций
|
|
Рассмотрим гидроакустические характеристики всех четырех высоконапорных
ГЭС из представленного ранее списка и добавим к ним еще две:
Токтогульскую гидроэлектростанцию на реке Нарын в Киргизии [54] и
строящуюся на реке Ланканг (китайское название верховьев Меконга) ГЭС
Сяовань (Xiaowan) [49, 55 – 58], первый гидроагрегат которой должен
начать работу в конце 2010 года. Высота бетонной гравитационной плотины
Токтогульской ГЭС составляет 215 м, а высота арочной плотины ГЭС
Сяовань – 292 м. |
|
Однако прежде, чем приступить к рассмотрению характеристик этих
гидроэлектростанций, введем численный параметр, характеризующий степень
возбуждаемости гидроакустических автоколебаний в напорном водоводе или,
иными словами, индекс устойчивости работы напорной системы. Как
известно, у автоколебательных систем могут быть мягкие и жесткие режимы
возбуждения [53]. В первом случае любое случайное малое колебание
запускает процесс автоколебаний, во втором интенсивность возмущения
должна быть не ниже некоторой критической величины. Так как за всю
историю гидроэнергетики пока известно только 2 случая запуска
автоколебаний в водоводах, следует сделать вывод о том, что в данном
случае возбуждение жесткое. Из имеющихся опытных данных попробуем
оценить условия, при которых внешние колебания могут запустить процесс
автоколебаний. |
|
Как понятно из предыдущих разделов, гидроакустическая автоколебательная
система запускается под воздействием внешнего возмущения при близости
собственной частоты с его частотой, которая может быть либо
турбинной νr, либо вихревой
частотой νv. При этом степень
воздействия внешнего
возмущения зависит как от его интенсивности, так и от разницы
собственной и возбуждающей частот. Вследствие подобия процессов можно
полагать, что относительная интенсивность возмущений, необходимая для
запуска автоколебаний везде примерно одинакова, и первостепенным по
важности оказывается резонансный отклик колебательной системы на
«стандартное» внешнее возмущение. Поэтому именно оценка резонансного
отклика еще невозбужденной колебательной системы с затуханием (степень
жесткости запуска автоколебаний) должна лежать в основе оценки ее
гидроакустической устойчивости. |
|
Как известно, полуширина частотного диапазона Δν, на которой амплитуда
резонансного возбуждения колебательной системы с затуханием уменьшается
в √2 раз по сравнению с максимумом, при малых величинах степени
затухания δ определяется следующим выражением [45, 53]: |
|
|
| где νe
– резонансная частота
колебательной системы. |
|
Для рассматриваемой системы частота возмущения νp
– либо турбинная νr,
либо вихревая νv. Коэффициент затухания
определяется в точке экстремума
расходной характеристики турбины, и, поэтому, δ = δ1,
и,
соответственно, β = β1 (см. раздел VII). Так как
уровень возмущения,
необходимого для возбуждения автоколебаний пока неизвестен, в выражение
(30) введем коэффициент σ, критическая величина которого,
соответствующая нижней границе зоны запуска автоколебаний, будет
определяться из имеющихся экспериментальных данных. Для удобства
нормирования величины σ введем также в выражение (30) коэффициент 5: |
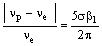 |
| Отсюда |
|
|
или
|
|
|
| где θ – добротность
колебательного контура |
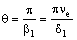 |
|
Теперь параметр σ, называемый далее индексом устойчивости
гидроакустической системы, характеризует степень резонансного отклика
колебательной системы, состоящей из напорного водовода, турбины и
отсасывающей трубы, на внешнее колебательное возмущение. Уровень
отклика, при котором система в процессе жесткого возбуждения переходит
в автоколебательный режим, может быть приблизительно оценен из
имеющихся натурных данных: по крайней мере, в двух случаях этот режим
был запущен, во многих других – нет. Для всех этих случаев можно
подсчитать индекс устойчивости, и граница раздела между ними даст
критический уровень индекса σ*. Критерием возбуждения окажется условие |
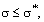 |
| при этом критический уровень
индекса σ* определяется из эмпирических данных. |
|
Сначала вернемся к данным таблицы 9 и по формулам (31) или (32)
подсчитаем индекс устойчивости σ в точках максимумов кривой Δp/p, с
которых произошел запуск автоколебаний водоводов на Нурекской и
Саяно-Шушенской ГЭС. Полученные результаты представлены в последнем
столбце этой таблицы: для СШ ГЭС индекс устойчивости на режиме работы,
который привел к катастрофе, оказался равен σ = 0.60 ± 0.12 вследствие
разброса в оценке вихревой частоты νv,
а для Нурекской ГЭС
предаварийный индекс для первого гидроагрегата σ = 0.55 ± 0.45. Здесь
разброс расчетных значений индекса устойчивости оказался почти в 4 раза
больше вследствие существенно меньшей точности экспериментальных данных
по вихревой частоте в зоне A (см., [11, 12]). Таким образом, при
уровнях индекса устойчивости 0.5 – 0.7 и 0.1 – 1.0 дважды происходил
запуск автоколебаний в напорных системах. Следует также отметить
близость средних значений индекса устойчивости (0.6 и 0.55) для
напорных систем, сильно отличающихся по своим параметрам, и для
аварийных ситуаций, возникших на разных режимах их работы. Это является
свидетельством правильности проводимых оценок. |
|
Перейдем теперь к рассмотрению гидроакустической устойчивости других
высоконапорных гидроэлектростанций. Надо отметить, что длины водоводов
Саяно-Шушенской и Нурекской ГЭС точно известны. Для Чиркейской ГЭС
расчеты были проведены для двух различных длин водоводов, там
имеющихся (см. [51, 59]. Длина водоводов на ГЭС Гувер была
определена по находящимся в свободном доступе схемам [22]. Для
Токтогульской
ГЭС использовались оценки длин водоводов через их корреляцию по
минимальному напору с водоводами известных размеров (по аналогии с
Саяно-Шушенской и Чиркейской ГЭС) и с учетом рядного расположения
гидроагрегатов, поэтому точность таких оценок не очень велика. Хотелось
провести оценки гидроакустической устойчивости хотя бы одной из многих
строящихся сейчас новых китайских гидроэлектростанций с высоконапорными
плотинами, однако необходимых для этого данных по ним нет. Поэтому была
выбрана ГЭС Сяовань с арочной плотиной двойной кривизны, которая, в
принципе, подобна плотине Чиркейской ГЭС, и с последней был проведен
пересчет длин водоводов по высоте плотины. Однако нет никаких оснований
утверждать, что на ГЭС Сяовань водоводы расположены так же как на
Чиркейской ГЭС по внешней поверхности плотины. Поэтому данный
умозрительный вариант был назван Сяовань’, и до получения реальной
информации о конструкции и длине водоводов станции он может
рассматриваться только как модельный расчетный пример возможности
гидроакустической неустойчивости при классической компоновке водоводов
на такой высотной плотине. |
|
Результаты расчетов автоколебательных процессов для шести
высоконапорных ГЭС представлены в таблице 11. Во всех случаях
рассматривался режим возбуждения автоколебаний в зоне A’, который
приводит к катастрофическому сценарию дальнейшего развития событий. Для
Саяно-Шушенской ГЭС повторены две верхние строки из таблицы 9. Для
Нурекской ГЭС из-за большой длины ее водоводов режим был рассчитан на
второй моде колебаний (рассмотрены самый длинный (третий) и самый
короткий (восьмой) водоводы, а также водовод первого гидроагрегата, на
котором ранее произошла авария в режиме возбуждения первой моды
колебаний). Для гидростанций Гувер и Токтогульской вычислены значения
индекса σ для частот возбуждения как вихревой, так и турбинной, а для
остальных – только для вихревой частоты, так как турбинные частоты там
гораздо удаленнее от частот собственных колебаний водовода, и никакой
опасности собой не представляют. |
|
Прямым жирным шрифтом в этой таблице выделены неустойчивые
гидроэлектростанции в зоне A’ (Нурекская ГЭС оказалась неустойчивой в
зоне A), а косым жирным шрифтом – ГЭС, приближающиеся к границе
устойчивости и, видимо, могущие ее перейти при очень сильных
возмущениях, вносимых в работу их гидроагрегатов. |
|
| Таблица
11 |
| N |
L1 (м) |
L2 (м) |
κ |
νe
(Гц) |
β |
νp
(Гц) |
σ |
|
| СШ |
241 |
28 |
0.035 |
1.55 |
0.172 |
1.425 ± 0.025 |
0.60 ± 0.12 |
| 0.050 |
1.60 |
– 0.672 |
|
|
| Нурекская* |
666 |
34.5 |
0.055 |
1.59 |
0.152 |
2.00
± 0.04 |
2.1
± 0.2 |
| 0.070 |
1.60 |
– 0.565 |
|
| 649 |
34.5 |
0.055 |
1.63 |
0.149 |
2.00
± 0.04 |
1.9
± 0.2 |
| 0.070 |
1.64 |
– 0.547 |
|
| 610 |
34.5 |
0.055 |
1.73 |
0.141 |
2.00 ± 0.04 |
1.4 ± 0.2 |
| 0.070 |
1.74 |
– 0.507 |
|
|
| Гувер** |
115 |
30 |
0.095 |
3.29 |
0.074 |
1.80 ± 0.03 |
7.7
± 0.2 |
| 0.110 |
3.33 |
– 0.297 |
3.00 |
1.5 |
|
| 100 |
30 |
0.095 |
3.73 |
0.071 |
1.80 ± 0.03 |
9.2
± 0.15 |
| 0.110 |
3.76 |
– 0.232 |
3.00 |
3.5 |
|
|
| Чиркейская |
226 |
32 |
0.035 |
1.63 |
0.143 |
2.00
± 0.04 |
2.0
± 0.2 |
| 0.050 |
1.67 |
– 0.461 |
|
| 205 |
60.7 |
0.035 |
1.72 |
0.137 |
2.00 ± 0.04 |
1.5 ± 0.2 |
| 0.050 |
1.74 |
– 0.121 |
|
|
| Токтогульская** |
175 |
30 |
0.035 |
2.07 |
0.126 |
1.66 ± 0.03 |
2.0
± 0.15 |
| 0.050 |
2.12 |
– 0.317 |
2.78 |
3.4 |
|
| 155 |
55 |
0.035 |
2.25 |
0.121 |
1.66 ± 0.03 |
2.7
± 0.15 |
| 0.050 |
2.28 |
– 0.040 |
2.78 |
2.4 |
|
|
| Сяовань’ |
275 |
30 |
0.035 |
1.37 |
0.231 |
1.50 ± 0.03 |
0.5 ± 0.1 |
| 0.050 |
1.41 |
– 0.857 |
|
|
| * – гидроакустическая
устойчивость рассматривается на второй моде собственных колебаний. |
| ** – устойчивость
рассматривается для возбуждающих колебаний, как с вихревой, так и с
турбинной частотами. |
В таблицах 9 и 11 всего рассмотрено 4 качественно различных режима
возможного возбуждения автоколебаний:
- возбуждение в зоне A первой
моды собственных колебаний на вихревой частоте;
- возбуждение в зоне A’ первой
моды собственных колебаний на вихревой частоте;
- возбуждение в зоне A’ второй
моды собственных колебаний на вихревой частоте;
- возбуждение в зоне A’ первой
моды собственных колебаний на турбинной частоте.
|
| Как показали предварительные
оценки длин водоводов для возбуждения третьей и четвертой мод
собственных колебаний, такие режимы также могут иметь практический
интерес при использовании высокоскоростных гидроагрегатов или в
некоторых специальных условиях, которые могут иметь место на
гидроаккумулирующих станциях. Тогда, в принципе, расчетных вариантов
режимов устойчивости может быть не менее 12: это число получается при
суммировании произведения четырех мод на две частоты внешнего
возбуждения в зоне A’ стационарной характеристики турбины, и двух мод
на те же две частоты в зоне A. Все эти 12 вариантов возбуждения
автоколебаний на высоконапорных ГЭС надо рассматривать как потенциально
возможные в каждом конкретном случае, хотя, как правило, большинство из
них исключается практически сразу же при самом первом рассмотрении.
Если же рассматривать насосно-турбинные агрегаты гидроаккумулирующих
станций, то в насосном режиме у них также возможна неустойчивость в
зоне B, и тогда к рассмотрению надо принимать уже, как минимум, 20
вариантов неустойчивостей. |
|
Как известно, ни на одной работающей гидроэлектростанции, кроме
Саяно-Шушенской, не происходило возбуждения автоколебаний в водоводе в
зоне A’ (см. рис. 1), то есть при расходе воды большем, чем на рабочем
режиме, когда это означает катастрофическую раскачку пульсаций
давления. То есть все рассмотренные станции (кроме варианта Сяовань’,
который является чисто расчетным) настолько устойчивы на этом режиме,
что уровень критических для запуска возмущений на них не был достигнут,
и их можно считать, по крайней мере, условно устойчивыми. Минимальные
индексы устойчивости среди них равны 1.4 – 1.5 (восьмой агрегат на
Нурекской ГЭС с самым коротким водоводом длиной 610 м и агрегаты с
водоводами большей полной длины на Чиркейской ГЭС и Гувер, см. таблицу
11). Неустойчивые
режимы реализовывались при 0.1 < σ < 1.0.
Понятно, что граница между устойчивыми и неустойчивыми режимами не
является абсолютной, а в зависимости от интенсивности возмущения,
вносимого, например, автоматической системой управления лопатками
направляющего аппарата с ошибочным алгоритмом, может сдвигаться – чем
сильнее возмущение, тем при бóльших значениях σ находится граница
устойчивости системы к внешнему воздействию. Тем не менее, пока не
получена дополнительная информация (пока не произошел новый инцидент),
на основании анализа данных таблиц 9 и 11 можно считать, что граница
между устойчивыми и неустойчивыми режимами лежит при приблизительно при
σ = 1 – 1.5. Причем при σ < 1 по опыту известных инцидентов
система должна считаться абсолютно неустойчивой, а при σ = 1 –
1.5 –
потенциально опасной в эксплуатации. Абсолютная неустойчивость
означает, что при достаточно длительной эксплуатации станции наверняка
возникнут условия потери устойчивости напорной системы, приводящие, как
минимум к крупной аварии. При σ > 1.5 – 2 серьезных оснований
для беспокойства, видимо, быть не должно. Отсюда следует критерий
возбуждения гидроакустических автоколебаний напорной системы |
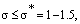 |
| где σ* – критическое значение
индекса устойчивости напорных систем. Гидроакустическая устойчивость
модельного варианта ГЭС Сяовань’ оказалась даже ниже уровня
устойчивости Саяно-Шушенской ГЭС. При этом у данного варианта ГЭС рост
амплитуды пульсаций за период, то есть интенсивность развития
катастрофического процесса, больше чем у СШ ГЭС (2.4 против 2.0). |
|
В дальнейшем
были проведены расчеты для трех гидроаккумулирующих станций,
позволившие снизить верхнюю границу критического значения индекса
устойчивости напорных систем до величины 1.2 [60]. Поэтому более точным
определением критического значения индекса является следующее: |
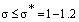 |
|
Для того чтобы повысить точность и надежность оценок гидроакустической
устойчивости ГЭС, необходимо получить точные геометрические параметры
водоводов некоторых из рассмотренных ГЭС, а также натурные данные о
добротности водоводов и о частоте прецессии вихревого шнура (вихревой
частоте) каждого из агрегатов на режимах не рекомендованной и
запрещенной работы. Это позволило бы уточнить описанные в работе
расчетные модели и повысить точность прогноза уровня их
гидроакустической устойчивости. Было бы также чрезвычайно полезно для
более точного определения границ гидроакустической устойчивости
провести натурные эксперименты по исследованию поведения на повышенных
мощностях третьего и восьмого агрегатов Нурекской ГЭС и одного из
агрегатов с длинными напорными водоводами Чиркейской ГЭС и ГЭС Гувер. |
|
Однако самым простым было бы получение информации о гидроагрегатах и
водоводах, а также о происходивших ранее инцидентах, видимо, с двух –
трех десятков имеющихся в мире высоконапорных гидроэлектростанций с
радиально-осевыми турбинами средней и большой мощности, индекс
гидроакустической устойчивости которых может оказаться не слишком
велик. Не менее интересно получить и проанализировать технические
данные о строящихся и проектируемых ГЭС такого же типа, количество
которых сопоставимо с количеством уже существующих станций. Автору
представляется, что наиболее заинтересованными в этом должны быть сами
эксплуатанты и проектировщики данных объектов. |
|
Выводы
|
- Построена теория локального
подобия для натурных радиально-осевых
гидротурбин средней и большой мощности, позволяющая пересчитывать их
вихревые частоты с одной турбины на другую.
- Найден простой метод оценки
собственных частот напорных водоводов.
- В результате решения
волнового уравнения с разрывным граничным
условием, моделирующим турбину, получен критерий возбуждения
автоколебаний и дан способ оценки гидроакустической устойчивости ГЭС.
- На основе предложенной
композитной теории объяснен ход событий в
двух инцидентах со срывом турбинной крышки на Нурекской и
Саяно-Шушенской гидроэлектростанциях.
- Вычислены индексы
гидроакустической устойчивости девяти гидроэлектростанций (для 22
наборов характеристических параметров), и к двум ГЭС, на практике
продемонстрировавшим свою неустойчивость, добавлены еще две станции с
низким уровнем гидроакустической устойчивости.
- Модельный вариант строящейся
в настоящее
время китайской гидроэлектростанции Сяовань’ оказался более
неустойчивым, чем Саяно-Шушенская ГЭС. Для оценки ее реальных
гидроакустических характеристик необходимы точные проектные данные, в
первую очередь, о длине напорных водоводов и отсасывающих труб этой
гидроэлектростанции.
|
| |
Ссылки
|
- Саяно-Шушенская ГЭС им. П. С.
Непорожнего. Новости.
РусГидро //
http://www.sshges.rushydro.ru/press/news/7660.html
- И. Малкова, А. Перетолчина –
Штатная ситуация. Ведомости,
05.10.2009, 187 (2457) //
http://www.vedomosti.ru/newspaper/article/2009/10/05/215438
- Ю. И. Лобановский –
Технические причины катастрофы на
Саяно-Шушенской ГЭС (итоги расследования), ноябрь 2009//
http://synerjetics.ru/article/catastrophe.htm
- Ю. И. Лобановский – Иерихон
на Енисее. ТехНАДЗОР,
N 11 (36), ноябрь 2009 //
http://www.synerjetics.ru/article/ierihon.pdf
- Акт технического
расследования причин аварии, произошедшей 17
августа 2009 года в филиале Открытого Акционерного Общества «РусГидро»
– «Саяно-Шушенская ГЭС имени П. С. Непорожнего» //
http://www.gosnadzor.ru/news/aktSSG___bak.doc
- На Саяно-Шушенской ГЭС
найдено тело последнего погибшего. Yтро.ru,
23.09.2009 //
http://www.utro.ru/news/2009/09/23/840266.shtml
- Саяно-Шушенская экономия. Газета.ru.
30.11.2009 //
http://www.gazeta.ru/business/2009/11/30/3293029.shtml
- Прайм-ТАСС, 19.08.09 //
http://www.prime-tass.ru/news/0/%7B7869A075-09D3-40E7-8EAC-CAB1E1034196%7D.uif
- Ростехнадзор назвал
предварительную версию аварии на
Саяно-Шушенской ГЭС. КоммерсантЪ, N 155 (4130), 25.08.2009 //
http://www.kommersant.ru/doc.aspx?DocsID=1226173&NodesID=6
- В. Л. Окулов, И. М. Пылев –
Неустойчивость напорных систем. Доклады
Академии наук, Энергетика, 1995, том 341, N 4.
- В. Х. Арм, В. Л. Окулов, И.
М. Пылев – Неустойчивость
напорных систем гидроэнергоблоков. Известия Академии
Наук, Энергетика, 1996.
- В. И. Брызгалов – Из опыта
создания и освоения Красноярской и
Саяно-Шушенской ГЭС. Производственное издание, 1998 //
http://03-ts.ru/index.php?nma=downloads&fla=stat&idd=826
- Д. Кюхеман – Аэродинамическое
проектирование самолетов. Москва,
Машиностроение, 1983.
- Л. Г. Лойцянский – Механика
жидкости и газа. Москва,
Наука, 1978.
- В. Н. Тарасов – Вибрации и
гидродинамическая устойчивость
гидроагрегата, 2009 //
http://www.diamech.ru/notes03112009.html
- Л. И. Седов – Механика
сплошной среды, т. 2. Москва,
Наука, 1976.
- Технические средства
диагностики. РусГидро, НИИЭС
//
http://www.niies.ru/works/technical_diagnostic_tools/uzr.php
- Форма 17. Станционный узел
(для гидроэлектростанций). Факс
из «Барки Точик» ОАХК, 07.12.2009.
- «Турбоатом» и таджикская
«Барки Точик» договорились… 02.11.2009
//
http://stocks.investfunds.com.ua/news/19817/
- Б. Сирожев: Авария на Нуреке
в 1983 году не была засекречена.
CAWATERiunfo, 26.10.2009 //
http://www.cawater-info.net/news/10-2009/26.htm
- Чиркейская ГЭС. РусГидро.
Дагестанский филиал //
http://www.dagestan.rushydro.ru/hpp/chirkey
- Hoover Dam. Wikipedia
//
http://en.wikipedia.org/wiki/Hoover_Dam
- Hoover Dam. National
Geographic Channel //
http://natgeotv.com.au/programmes/hoover-dam/photos
- Hoover Dam Turbine Runner. The
Historical Marker
Database //
http://www.hmdb.org/marker.asp?marker=1413
- Hoover Dam Frequently Asked
Questions and Answers. Hydropower
at Hoover Dam. U. S. Department of Interior. Bureau of
Reclamation //
http://www.usbr.gov/lc/hooverdam/faqs/powerfaq.html
- Hoover Dam Frequently Asked
Questions and Answers. Tunnels,
Towers, Penstocks and Spillways. U. S. Department of
Interior. Bureau of Reclamation //
http://www.usbr.gov/lc/hooverdam/faqs/tunlfaqs.html
- William M. Bruninga –
Equipment: Turbine Improvements at
Hoover Dam //
http://www.hydroworld.com/index.html
- S. R. Turns – Thermodynamics:
Concepts and Applications, 2006
//
http://www.cambridge.org/us/catalogue/catalogue.asp?isbn=9780521850421
- Itaipu. Wikipedia
//
http://en.wikipedia.org/wiki/Itaipu
- S. Krauter – Itaipu //
http://www.solar.coppe.ufrj.br/itaipu_conv.html
- Krasnoyarsk hydroelectric
dam. Wikipedia //
http://en.wikipedia.org/wiki/Krasnoyarsk_hydroelectric_dam
- Гидрогенератор. БСЭ.
Яндекс, энциклопедии //
http://slovari.yandex.ru/dict/bse/article/00018/22900.htm
- Three Gorges Dam. Wikipedia
//
http://en.wikipedia.org/wiki/Three_Gorges_Dam
- HyPower. Customers Magazine
for Voith Siemens Hydro. August
2003 //
http://www.voithhydro.com/media/vs_SD_hypo_FinalVersion.pdf
- Three Gorges Dam. Wikipedia@pedia
//
http://wikipedia.atpedia.com/en/articles/t/h/r/Three_Gorges_Dam_1276.html
- 8.3. Гидрогенераторы. 8.3.1.
Классификация гидрогенераторов. Ремонт
электродвигателей //
http://www.motor-remont.ru/books/book1/book1p44.htm
- Kaplan turbine. Wikipedia
//
http://en.wikipedia.org/wiki/Kaplan_turbine
- Deriaz turbine. Wikipedia
//
http://www.daviddarling.info/encyclopedia/D/AE_Deriaz_turbine.html
- Francis turbine. Wikipedia
//
http://en.wikipedia.org/wiki/Francis_turbine
- Pelton wheel. Wikipedia
//
http://en.wikipedia.org/wiki/Pelton_wheel
- Гидравлические турбины. Силовые
машины //
http://www.power-m.ru/themes/basic/prod-index.asp?folder=1242
- Water turbines. Encyclopedia
Britannica //
http://www.britannica.com/EBchecked/topic/609552/turbine/45661/Water-turbines
- Диагональная турбина. Словари
и энциклопедии на
Академике //
http://dic.academic.ru/dic.nsf/bse/84288/Диагональная
- РусГидро. Саяно-Шушенская ГЭС
им. П. С. Непорожнего.
Гидротурбинное (оборудование) //
http://www.sshges.rushydro.ru/hpp/units/hydro
- Г. С. Горелик – Колебания и
волны: введение в акустику,
радиофизику и оптику. Москва, Государственное
издательство физико-математической литературы, 1959.
- В. Л. Окулов – Прецессия
винтового вихревого жгута как
возбудитель резонансов в напорных системах. Выписка
из протокола семинара Института теплофизики, 20.11.2009.
- В. С. Селезнев – Частное
сообщение. 20.01.2010.
- Экспериментируем с созданием
звука и музыка. Некоторые
результаты исследований //
http://corpuscul.net/teoriya-zvuka-2/akusticheskie-xarakteristiki-orkestra/duxovye-akustika/nekotorye-rezultaty-issledovanij/
- A. Schwery – Large Hydro
Generators. Experience and
References. ALSTOM, 27.08.2008 //
http://www.cigre-a1.org/Site/Events/download/11-ALSTOM%20CIGRE%202008%20Rev1ID31VER36.pdf
- Схема (разрез)
Саяно-Шушенской ГЭС. News2 //
http://news2.ru/story/187262/
- Чиркейская ГЭС //
http://dic.academic.ru/dic.nsf/ruwiki/100918
- Дж. В. Стретт (Лорд Рэлей) –
Теория звука, т. II. Москва,
Государственное издательство технико-теоретической литературы, 1955.
- Н. В. Карлов, Н. А. Кириченко
– Колебания, волны, структуры. Москва,
Физматлит, 2001.
- Токтогульская ГЭС. ОАО
«Электрические станции» //
http://www.energo-es.kg/stations/hps/toktogul/
- Xiaowan Dam. Wikipedia
//
http://en.wikipedia.org/wiki/Xiaowan_Dam
- M. Richardson – Dams in China
Turn the Mekong Into a River of
Discord: Rivers Know No Borders, But Dams Do. The
Asia-Pacific Journal: vol. 35-1-09, August 31, 2009 //
http://www.japanfocus.org/-Michael-Richardson/3210
- Китай пошел против течения. Бюджет.ru.
Новости.
19.10.2009 //
http://bujet.ru/article/64684.php
- Fu Bingjun, P. Grasso, Xu
Shulin – Construction of
Underground Hydraulic Structures and TBM Technology in China. Chinese
Journal of Rock Mechanics and Engineering, 2003 //
http://www.rockmech.org/qikan/manage/wenzhang/2003-09-23.pdf
- Чиркейский
гидроузел. Ленгидропроект //
http://www.regtime.spb.ru/lenhydroproject/chirkey.html
- Ю. И. Лобановский –
Гидроакустическая устойчивость гидроакуумулирующих станций, январь 2010 //
http://synerjetics.ru/article/stability.htm
|
| |
| Благодарю А. Е. Бражникова, И.
А. Мерзликина, Д. В. Степанова и О. В. Федяева за полезное участие в
этой работе. |
| |
| 10.01 –
10.02.2010, 06.12.2010
Ю. И. Лобановский |
| |
|
| |
|