SYNERJETICS GROUP Эффективное выведение полезных нагрузок на низкую околоземную орбиту многоразовой аэрокосмической транспортной системой. Обеспечение дальности полета на параллакс 3000 км, и до 6500 км до зоны пуска второй ступени при дозаправке горючим с дозвукового транспортного самолета. Возможны практически любые углы наклонения орбит выводимых полезных нагрузок.

Главная страница

Цели освоения космоса

Миссия космонавтики

Кризис цивилизации

На распутье

Программа освоения космоса

Хранилище на орбите

Орбитальная медицина

Аэрокосмические носители

Описание концепции

Обоснование концепции

Анализ эффективности

Обратная связь

Концепция перспективной аэрокосмической
транспортной системы

Ю. И. Лобановский

Центральный Аэрогидродинамический Институт имени проф. Н. Е. Жуковского

Препринт ЦАГИ, N 95, 1994

Краткое содержание

В работе рассматривается комплекс основных проблем, которые препятствуют созданию в ближайшем будущем одноступенчатого аэрокосмического самолета. Проанализированы особенности двухступенчатого аэрокосмического носителя типа Sänger, не способного вывести на околоземную орбиту достаточно большую полезную нагрузку. Предлагаются альтернативная схема полностью многоразового двухступенчатого аэрокосмического самолета и новые решения в гиперзвуковой аэродинамике и схемах воздушно-реактивных двигателей. Эти инновации могут существенно увеличить эффективность такого аппарата как транспортного средства. Исследуется также возможность применения дозвукового самолета-заправщика для разрешения противоречия между гибкостью и эффективностью аэрокосмических транспортных систем.

Предлагаемая космическая транспортная система Star Liner, состоящая из полностью многоразового двухступенчатого аэрокосмического самолета и, в случае необходимости, дозвукового самолета-заправщика, позволяет, по предварительным оценкам, выводить на низкую околоземную орбиту полезные нагрузки, составляющие 8 - 12 % от стартовой массы аэрокосмического самолета при дальности полета на параллакс 3000 - 6500 км. Следовательно, относительная масса ее полезной нагрузки в 5 - 10 раз больше, чем у других известных полностью многоразовых космических транспортных систем, таких как Sänger или Delta Clipper. Дозаправка топливом, применяемая в случае больших расстояний от аэродрома до зоны пуска второй ступени, позволяет устранить практически любые ограничения на углы наклонения орбит выводимых полезных нагрузок.

Введение

Создание многоразовых аэрокосмических транспортных систем является в настоящее время одной из актуальных научно-технических проблем, стоящих перед человечеством. Однако следует помнить, что это уже вторая попытка добиться успеха в более сложной, чем она представляется на первый взгляд, области технологии. Первая, романтическая попытка создания многоразовых гиперзвуковых и аэрокосмических аппаратов на волне общественного и технологического оптимизма начала второй половины XX века и ранних успехов ракетной техники, космонавтики и сверхзвуковой авиации хотя и привела в итоге к созданию частично многоразовых аэрокосмических систем Space Shuttle и "Буран", но достигнутые результаты отличаются от мечтаний тридцатилетней давности (см., например, [1]) примерно так же, как и реальные достижения в области термоядерного синтеза от ожиданий его пионеров, в то же самое время закладывавших основы будущего энергетического изобилия человечества.

Резкая активизация работ в области гиперзвуковых технологий началась снова несколько лет назад, что в первую очередь связано с принятием в США в 1986 году программы NASP, предусматривавшей создание экспериментального одноступенчатого аэрокосмического самолета (АКС) X-30. Это сразу же оживило аналогичные исследования и разработки практически во всех государствах с достаточно развитой аэрокосмической промышленностью. Прошедшие с тех пор 7 лет предоставили немало оснований для критического анализа положения дел в этой области. По первоначальным планам первый полет X-30 должен был состояться в 1993 году [2], и именно к этому времени стал осуществляться коренной пересмотр программы NASP. Вместо полноразмерного самолета X-30 для проведения исследований предлагается создать два небольших и существенно более простых экспериментальных аппарата [3,4].

Программа создания британского АКС Hotol после кардинального пересмотра концепции [5] в настоящее время весьма близка к закрытию. Реализация планов создания немецкого (европейского) АКС Sänger значительно более вероятна, однако и эта программа оценивается сейчас как слишком дорогостоящая [6]. Ситуация с аэрокосмическими программами в России, несмотря на существование целой гаммы различных проектов [7], близка к критической. В мае 1993 года принято решение о закрытии программы "Буран". Во Франции и Японии исследования в области гиперзвуковых технологий пока не вышли за рамки предварительного изучения различных концепций. Таким образом, очевиден очередной кризис в области аэрокосмических технологий, преодоление которого необходимо для эффективного решения многих актуальных задач космонавтики.

Для разрешения этого кризиса следует, возможно, более четко выявить цели и пути их достижения, основные препятствия и возможности их преодоления, технологии, критически важные для создания АКС, и ресурсы, которые общество согласно затратить на эти исследования и разработки. Все это возможно сделать путем международного публичного обсуждения, в котором могут принять участие все заинтересованные стороны, тем более, что политическая ситуация в мире впервые благоприятствует этому. Предлагаемая статья и является попыткой начать такую дискуссию. Известными основаниями для принятия на себя этой миссии автор считает, во-первых, то, что критическая часть статьи полностью основана на неопубликованной работе, написанной им 5 лет назад, во времена, когда ближайшие перспективы одноступенчатого аэрокосмического самолета X-30 оценивались научным сообществом значительно более оптимистично, чем сейчас, а во-вторых, то, что, по мнению автора, рациональное применение уже существующих и активно изучаемых технологических решений позволит создать аэрокосмическую транспортную систему на порядок более эффективную, чем разрабатываемые в настоящее время.

2. Основные проблемы создания одноступенчатого аэрокосмического самолета

Основным преимуществом аэрокосмического самолета перед многоразовым ракетным аппаратом является возможность примерно на порядок увеличить максимальный удельный импульс двигательной установки за счет использования атмосферного воздуха [8,9]. Поэтому априори наиболее перспективной компоновочной схемой представляется одноступенчатая схема АКС типа NASP, где эта возможность в принципе реализуется наиболее полно. Кроме того, одноступенчатый аппарат, очевидно, наиболее прост в эксплуатации. Однако за эти преимущества приходится дорого платить. Исследования последнего времени очертили круг ключевых проблем, которые необходимо решить для создания одноступенчатого АКС. Не претендуя на полноту, отметим три комплекса проблем, которые являются критическими.

Во-первых, это аэродинамический нагрев АКС на траектории разгона. Траектория движения АКС в атмосфере должна обеспечивать эффективную работу воздушно-реактивных двигателей, что означает полет при максимально допустимом скоростном напоре практически на всем участке использования атмосферного воздуха. Величина скоростного напора должна быть не менее 50 - 70 кПа, что в 5 - 6 раз больше скоростного напора у дозвуковых лайнеров [10]. При этом внешние формы АКС должны обеспечивать приемлемые уровни аэродинамического качества и сопротивления, следовательно, аппарат будет тонким с относительно острыми носком и передними кромками крыла. Поэтому максимальные плотности тепловых потоков в критической точке на разгонной траектории достигнут 700 - 900 Вт/см², а полные тепловые нагрузки там же - 700 - 1100 кДж/см², что в 15 - 20 раз превышает значения соответствующих величин на траектории возвращения с околоземной орбиты аппарата типа Space Shuttle [11]. Максимальные равновесные температуры в критической точке и на передней кромке крыла могут составить соответственно 3500 К и 2600 К. Уровень тепловых нагрузок в критической точке при возвращении одноступенчатого АКС с орбиты будет в 2 - 3 раза больше, чем у аппарата Space Shuttle [11]. Таким образом, необходимость обеспечения эффективной работы воздушно-реактивных двигателей одноступенчатого АКС приводит к максимальным тепловым нагрузкам на траектории полета, более чем на порядок превосходящим максимальные тепловые нагрузки существующих воздушно-космических аппаратов, при достаточно больших силах, действующих на конструкцию.

Второй крупнейший комплекс проблем связан с созданием силовой установки одноступенчатого АКС. Ни один из современных воздушно-реактивных двигателей (ВРД) даже в принципе не способен работать во всем диапазоне скоростей от взлетной до орбитальной (числа Маха полета от 0 до 25). Более того, пока не ясно, возможна ли работа какого-либо типа ВРД при M > 15 - 16. Поэтому двигательная установка одноступенчатого АКС должна представлять собой более или менее интегрированный комплекс из 3 - 4 типов двигателей [8], и последовательная работа двигательных модулей аэрокосмического самолета должна заменить последовательную работу ступеней ракетных аппаратов.

Традиционный взгляд на эту проблему состоит в том, что в диапазоне скоростей полета, соответствующих M = 0 - 4, наиболее эффективны двигатели турбокомпрессорного типа (турбореактивные, ракетно-турбинные, в том числе и пароводородные). При M = 3 - 7 наилучшими характеристиками обладает прямоточный воздушно-реактивный двигатель с дозвуковым горением (ПВРД), при M ≥ 6 - 8 единственно возможно использование ПВРД со сверхзвуковым горением (ГПВРД), впервые испытанного в полете в ноябре 1991 года в России [12]. Когда число Маха полета превысит 15 - 16, окажется необходимым использование водородно-кислородного ракетного двигателя (РД) [8].

Хотя в принципе переход от режима дозвукового горения к сверхзвуковому в ПВРД может быть обеспечен изменением геометрии его внутреннего тракта и места впрыска водорода, так что силовая установка одноступенчатого АКС будет комбинацией скорее 3, чем 4 типов двигателей, однако для этого необходимо удовлетворить существенно противоречивым требованиям на границах рабочего режима двигателя, что в лучшем случае приведет там к ухудшению его характеристик. Испытания уменьшенной модели ГПВРД в США в 1991 году на режиме дозвукового горения при минимальной рабочей скорости показали значительно меньший уровень тяги, чем предполагалось [13]. Поэтому коэффициент полезного действия такого двухрежимного ПВРД будет ниже, чем у однорежимного ГПВРД, особенно или при малых, или при больших числах Маха. Кроме того, сложность конструкции такой комбинированной силовой установки намного превосходит все, что было создано в этой области до настоящего времени. Существенным фактором будет и достаточно большая масса такой установки.

Удельный импульс ГПВРД уменьшается с ростом числа Маха полета и по предварительным оптимистическим оценкам при M = 10 - 12 превосходит удельный импульс водородно-кислородного РД в 3 - 4 раза, а при M = 15 - 16 их удельные импульсы становятся соизмеримы (отсутствие возможности достаточно точно оценить характеристики ГПВРД при M > 12 вносит, вероятно, наибольший вклад в неопределенность характеристик одноступенчатого аэрокосмического самолета [8]).

Поэтому, применение ГПВРД при увеличении скорости полета обещает все меньшие выигрыши по сравнению с ракетным двигателем. Разработка двигателя, использующего сжиженный воздух, что позволило бы сократить число режимов работы и, соответственно, число модулей комбинированной силовой установки хотя бы и ценой уменьшения ее удельного импульса, встретилась, по-видимому, с фундаментальными трудностями [5].

В-третьих, необходимо, чтобы конструкция одноступенчатого АКС, от которой требуется, чтобы она работала при температурах от 20 К (температура жидкого водорода) до ~3000 К (равновесная температура в критической точке) и скоростных напорах в несколько раз больших, чем для дозвуковых самолетов, была беспрецедентно легкой. Известно упрощенное соотношение между коэффициентом заправочной массы f, средней по траектории величиной отношения тяги к сопротивлению P/X и Δe - отношением приобретенной аппаратом удельной энергии к удельной работе, произведенной силовой установкой АКС при разгоне [14]:

f = 1 - (1 - 0.5Δe/φ)/[1 + Δe(1 + 0.5/φ)] (φ > 0), (2.1)

где f = m_F/m, Δe = ΔE/ηQ, E = 0.5V² + gh, φ = P/X - 1, m_F - затраченная на разгон масса топлива, m - стартовая масса аппарата, V и h - соответственно скорость и высота на траектории полета, g - ускорение свободного падения, η - средний на траектории пропульсивный коэффициент полезного действия двигателей, Q - теплотворная способность топлива (для водорода Q = 1.2·10⁸ Дж/кг). Результаты расчетов по формуле (2.1) оказались в хорошем согласии с данными летных экспериментов на гиперзвуковом аппарате X-15 (M_max = 6.5 - 6.7, Δe ≈ 1) [14].

Для выхода на низкую околоземную орбиту даже в случае использования воздушно-реактивных двигателей на всех участках разгонной траектории, что очень проблематично, и при оптимистических оценках эффективности силовой установки аэрокосмического самолета (η = 0.4), коэффициент f составит не менее, чем 0.56, и доли массы конструкции и полезной нагрузки не должны превышать 0.44 от стартовой массы АКС [14] (см. рис. 1, кривая 1, точка 2). Кривая 3 соответствует одноступенчатому крылатому аэрокосмическому аппарату с горизонтальным стартом, использующему только водородно-кислородные ракетные двигатели, орбитальная масса которого будет не более 0.10 от стартовой, а относительная масса конструкции при больших размерах составит 0.16 - 0.20 от стартовой [15], что в 1.5 - 2 раза превосходит орбитальную. Следовательно, аппарат такого типа на орбиту выйти не сможет.

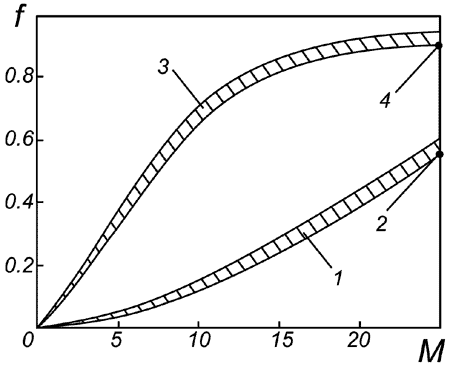Рис. 1

По-видимому, наиболее легкая современная авиационная конструкция - это выполненная из композиционных материалов и рассчитанная на низкие предельные перегрузки конструкция совершившего беспосадочный кругосветный перелет самолета Voyager. Доля ее в стартовой массе аппарата составляет 0.21. Однако, если баки этого самолета заполнить на порядок более легким, чем бензин или керосин, жидким водородом, коэффициент заправочной массы f не превысил бы 0.28 [14].

Безусловно, проектирование аппаратов, использующих в качестве топлива жидкий водород, а не керосин или бензин, осуществляется на основе иных подходов, чем проектирование самолета Voyager, однако даже если не учитывать относительно большую массу сложной силовой установки АКС, теплозащиту, покрывающую всю его внешнюю поверхность, теплоизоляцию баков криогенного водорода, и систему орбитального маневрирования, необходимость, по крайней мере, вдвое увеличить долю заправочной массы одноступенчатого АКС по сравнению с самолетом Voyager (то есть при той же массе конструкции увеличить объем баков в 3.3 раза), поставит перед разработчиками одноступенчатого АКС трудноразрешимые проблемы.

Таким образом, при создании одноступенчатого аэрокосмического самолета, по крайней мере, в трех областях технологии необходимо разрешить проблемы, сложность которых далеко превосходит все, достигнутое в этих областях до сих пор. Более того, существует тесная взаимосвязь этих проблем между собой, вносящая дополнительные элементы неопределенности и существенно ограничивающая возможности их решения.

Несмотря на значительный прогресс, достигнутый при разработке основных технологий по программе NASP, этот комплекс действительно фундаментальных трудностей, вставший перед разработчиками одноступенчатого аэрокосмического самолета, первоначально привел к переносу первого полета аппарата X-30 с 1993 [2] на 1997 год, далее на 2003 [16], потом к заявлению главного администратора NASA Д. Голдина о готовности управления прекратить осуществление программы NASP в пользу программы научных исследований в области гиперзвуковых скоростей [3], а затем и к прекращению финансирования разработки АКС X-30 [17].

3. Анализ классической схемы двухступенчатого аэрокосмического самолета

Проведенный выше обзор основных проблем, связанных с созданием одноступенчатого АКС, позволяет заключить, что технический риск разработки такого аппарата очень велик. Результаты первых семи лет программы NASP продемонстрировали, что при технологическом уровне ближайшего будущего такая компоновочная схема аэрокосмического самолета, по крайней мере, трудно реализуема. Поэтому представляется целесообразным более внимательно рассмотреть другие компоновочные схемы, одну из которых можно будет реализовать после проведения соответствующего комплекса научно-исследовательских и опытно-конструкторских работ. Кроме того, необходимо продолжить изучение фундаментальных проблем, решение которых может позволить по иному подойти к некоторым аспектам рассматриваемых технологий.

Очевидно, что использование двухступенчатой компоновочной схемы АКС значительно уменьшает трудности решения всех трех упомянутых выше комплексов проблем. Важнейшим параметром такого аэрокосмического самолета является скорость, при которой происходит разделение ступеней.

Как известно, для выхода аппарата на низкую околоземную орбиту необходимо достичь скорости 7.8 км/с. Так как разгон происходит в гравитационном поле и атмосфере планеты, для получения характеристической скорости разгонной операции необходимо добавить к указанной величине гравитационные и аэродинамические потери и потери на управление [18]. При стартовой тяговооруженности, характерной для современных ракет-носителей и составляющей 1.25 - 1.5, эти потери близки к величине 1.9 км/с. При запуске в восточном направлении и умеренной широте старта вращение Земли уменьшает характеристическую скорость на 0.3 - 0.45 км/с [18]. Таким образом, диапазон минимальных характеристических скоростей выхода на низкую околоземную орбиту в зависимости от условий старта составляет U = 9.2 - 9.4 км/с, причем практически все потери приходятся на нижний участок траектории, когда ее направление значительно отклоняется от трансверсального, плотность воздуха еще достаточно велика, а траектория достаточно искривлена.

Оптимальная скорость разделения ракетного аппарата, состоящего из двух ступеней с близкими характеристиками, близка к половине характеристической скорости, что имеет место при скорости полета около 3 км/с. Интересно отметить, что, несмотря на значительно большие потери, в первую очередь аэродинамические, при разгоне аэрокосмического самолета с первой ступенью, использующей воздушно-реактивные двигатели, и второй - ракетной, и сильно изменяющиеся на траектории характеристики его силовой установки, при отсутствии ограничений оптимальная скорость разделения его ступеней по ранним оценкам также составляет примерно 3 км/с [19], что приблизительно соответствует M = 10. Улучшение аэродинамических характеристик и эффективности силовой установки первой ступени АКС приведет к увеличению этой скорости. С другой стороны, M = 6.5 - 7 (V = 2 - 2.1 км/с) является рубежом, начиная с которого возможно использование только либо ГПВРД, либо водородно-кислородного РД. Возникающие при полете на такой скорости тепловые проблемы хотя и существенны, но просто несопоставимы с проблемами нагрева одноступенчатого АКС при М = 15 - 20. Максимальные плотности тепловых потоков составят не более 2 - 3 % от соответствующих величин для одноступенчатого аэрокосмического самолета [11]. Роль аэродинамиков в этом случае будет состоять не только в выявлении форм, способных уцелеть на разгонной траектории, но и в поиске геометрии аппарата, который может иметь действительно высокие аэродинамические характеристики при гиперзвуковых скоростях, что существенно расширит эксплуатационные возможности АКС.

При скорости разделения V = 2.1 км/с (M = 7) силовая установка первой ступени может представлять собой интегрированный комплекс только из двух типов двигателей хорошо отработанных схем. В принципе возможно и использование двигательной установки, способной работать в непрерывном режиме во всем диапазоне полетных чисел Маха от 0 до 7 [20]. Создание конструкции первой ступени двухступенчатого АКС облегчается тем, что нет никакой необходимости укладываться в лимит относительной массы конструкции, который надо выдерживать при создании одноступенчатого АКС. В частности, предполагается, что относительная масса первой ступени двухступенчатого аэрокосмического самолета Sänger без топлива составит 0.58 - 0.61 (f = 0.39 - 0.42) [21,22], то есть при одинаковой массе конструкции в ее баках может быть, по крайней мере, в 2 раза меньше водорода, чем в баках NASP. При этом планируется, что АКС Sänger сможет, в отличие от одноступенчатого аэрокосмического самолета, обеспечить выход второй ступени на орбиты с малыми наклонениями при старте в умеренных широтах (параллакс орбиты). Максимальные температуры нижней поверхности первой ступени двухступенчатого АКС в основном не превысят 700 - 1000 К [11,23], и ее конструкцию можно будет выполнить из жаростойких сплавов или алюминия с внешней теплоизоляцией и с использованием систем активного охлаждения [22,23].

Характеристическая скорость U второй ступени составит в этом случае 5.4 - 5.8 км/с. При удельном импульсе I водородно-кислородного РД 4.65 - 4.7 км/с [8,21] отношение конечной массы второй ракетной ступени m_e к ее стартовой массе m₂, обозначаемое z^-1 = m_e/m₂, где z - число Циолковского, в соответствии с известной формулой [18]:

z = exp(U/I), (3.1)

составит z^-1 = 0.3. Между параметрами z и f существует простая связь:

z^-1 + f = 1. (3.2)

Относительная масса конструкции многоразовой второй крылатой ракетной ступени АКС по статистическим данным будет находиться в диапазоне от 0.20 до 0.25 [15] в зависимости от уровня ее технического совершенства, а также от того, является ли она автоматической или пилотируемой. Следует отметить, что, в отличие от одноступенчатого аэрокосмического самолета с воздушно-реактивным двигателем, около 5/6 массы топлива будет приходиться на жидкий кислород, плотность которого более чем в 15 раз превосходит плотность жидкого водорода. Поэтому в данном случае такие величины относительной массы конструкции вполне реальны. Параметр конструктивного совершенства s, представляющий собой отношение массы конструкции аппарата и массы содержащегося в нем топлива к массе конструкции, будет около 4. Для существенно более простых и, вдобавок, одноразовых водородно-кислородных ракетных ступеней уже 25 лет назад параметр s достигал в некоторых случаях величины, близкой к 12 (Ступень S-II лунной ракеты Saturn-5, 1967 год [18]). Таким образом, если учесть запасы топлива для возвращения с орбиты (не менее 0.05 от посадочной массы), доля полезной нагрузки двухступенчатого аэрокосмического самолета типа Sänger составит приблизительно 0.03 - 0.08 от стартовой массы второй ракетной ступени АКС.

Следовательно, скорость разделения, соответствующая числу Маха M = 6.5 - 7, является приемлемым компромиссом, не предъявляющим чрезмерно высоких требований, как к первой, так и второй ракетной ступеням АКС, и позволяющим использовать обе ступени в достаточно благоприятных для них условиях. При этом исключается или переносится на существенно более поздний срок риск, связанный с разработкой ГПВРД, который в перспективе можно использовать на второй ступени такого аэрокосмического самолета. Все эти соображения и легли, очевидно, в основу немецкой концепции двухступенчатого АКС Sänger, которая по глубине проработки и степени обоснованности принимаемых решений уже может быть признана классической.

Не может быть никаких сомнений в том, что, в отличие от одноступенчатого аэрокосмического самолета типа NASP, подобная концепция АКС при надлежащих усилиях может быть реализована в недалеком будущем. Однако платой за резкое снижение технического риска являются малые полезные нагрузки, выводимые на околоземную орбиту аппаратом такого типа, что ставит под сомнение экономическую эффективность, а значит и целесообразность создания подобных двухступенчатых систем. Это связано в первую очередь с тем, что на вторую, ракетную ступень, двигатели которой обладают относительно низким удельным импульсом, приходится слишком большой участок разгонной траектории.

Как оценивалось выше, масса полезной нагрузки составит 3 - 8 % от стартовой массы второй ступени. Масса первой ступени таких систем при оптимальной скорости разделения, по оценкам, превосходит массу второй ступени не менее, чем в 2 раза [19]. Если необходим полет в приэкваториальные широты Земли для запуска космических аппаратов на орбиты с малыми наклонениями, стартовая масса первой ступени увеличивается еще более даже при меньшей, чем оптимальная, скорости разделения ступеней. Для АКС Sänger отношение стартовых масс первой и второй ступеней m₁/m₂ составляет примерно 2.25 [22]. Следовательно, на орбиту может быть выведено не более 1 - 2.5 % от стартовой массы двухступенчатого АКС рассматриваемой схемы.

Для увеличения возможностей аэрокосмического самолета Sänger предполагается создать два типа многоразовых вторых ступеней - пилотируемую Horus-M и облегченную автоматическую грузовую Horus-C, несущую бóльшую нагрузку, и в зависимости от задач полета использовать тот или иной вариант. При этом относительная доля полезной нагрузки может варьироваться в пределах 1 - 2 % [15,22]. Применение в перспективе второй ступени с комбинированной силовой установкой, состоящей из ГПВРД и водородно-кислородного ракетного двигателя, приведет к увеличению доли полезной нагрузки, однако при этом снова возникнет бóльшая часть проблем, отодвинувших реализацию одноступенчатого АКС за пределы предвидимого будущего. Кроме того, значительная неопределенность характеристик ГПВРД при M > 12 в настоящий момент сильно затрудняет оценку возможных как положительных, так и отрицательных последствий, вытекающих из принятия такого решения.

Следует отметить, что принятый к разработке в США в 1991 году многоразовый одноступенчатый орбитальный носитель Delta Clipper баллистического типа с водородно-кислородными ракетными двигателями и вертикальными взлетом и посадкой [24] по проекту должен выводить на низкие орбиты от полярной до орбит с умеренными наклонениями полезную нагрузку, составляющую от 1 до 2 % от его стартовой массы [25]. При этом данная разработка может, в основном, опираться на уже апробированные технические решения, и единственной действительно принципиальной трудностью является создание многоразовой полностью возвращаемой ракетной конструкции с параметром конструктивного совершенства s ≈ 12.5, как у одноразовой. Сроки выполнения программы и затраты на нее по оценкам существенно ниже, чем на аэрокосмические самолеты [24,25]. Правда, система Delta Clipper не может обеспечить на активном участке полета сколько-нибудь заметный параллакс орбиты полезной нагрузки. На рис. 1 точка 4 (f = 0.90 - 0.91) соответствует характеристикам носителя Delta Clipper.

Таким образом, экономические показатели двухступенчатого АКС рассматриваемой в этой части работы классической концепции будут не очень высокими, и поэтому вполне оправданна оценка аэрокосмического самолета Sänger руководителем отдела перспективных носителей ESA Х. Пфеффером как слишком дорогостоящего [6].

4. Принципиальное обоснование альтернативной схемы двухступенчатого аэрокосмического самолета

Исследования ключевой технологии для эффективного гиперзвукового полета - ГПВРД показывают, что для того, чтобы при M > 12 удельный импульс этого двигателя заметно превышал удельный импульс водородно-кислородного РД, необходимо обеспечить весьма совершенную конструкцию воздушно-реактивного двигателя. Даже при близких к идеальным воздухозаборнике и сопле величины удельного импульса ГПВРД и РД становятся приблизительно равными при M = 16 - 20, а при более вероятных уровнях совершенства ГПВРД эти числа Маха соответствуют M = 13.5 - 16 [8]. Очевидно, что вследствие значительно бóльшей средней плотности ракетного топлива оптимальное по массе выводимой полезной нагрузки переключение на ракетный режим должно происходить при меньшей скорости полета. При достижении M = 12 - 15 повышение температуры теплозащитного покрытия заставит увеличить скорость подъема, уменьшив тем самым скоростной напор, а, значит, и тягу воздушно-реактивных двигателей [10]. Следовательно, при скорости полета, соответствующей M = 12 - 12.5, достигается еще одна выделенная по технологическим условиям точка разгонной траектории, в которой целесообразно рассмотреть разделение ступеней двухступенчатого АКС, причем, как следует из вышесказанного, в ближайшей перспективе целесообразна только ракетная вторая ступень.

С учетом возрастания скорости звука на соответствующих высотах (H = 40 - 45 км) [26], скорость разделения ступеней составит V = 4 км/с. При этом характеристическая скорость второй ступени будет только 3.5 - 3.8 км/с, что приводит к значительному увеличению ее полезной нагрузки. Если удельный импульс водородно-кислородного ракетного двигателя - 4.7 км/с, то соотношение конечной и стартовой масс второй ступени в соответствии с формулой (3.1) будет равно z^-1 ≥ 0.45, что в 1.5 раза выше, чем при разделении ступеней при M = 6.5 - 7. Если запуск происходит в восточном направлении в окрестности экватора, то вследствие вращения Земли характеристическая скорость второй ступени уменьшится до 3.35 км/с, а конечная масса второй ступени будет равна половине стартовой (z^-1 = 0.5). При той же относительной массе конструкции второй ступени, что и у АКС типа Sänger, полезная нагрузка составит 0.18 - 0.27 от стартовой массы второй ступени, что в 3 - 6 раз превысит показатель второй ступени аэрокосмического самолета классической схемы.

Вторая ступень предлагаемого аэрокосмического самолета по конструкции может быть практически идентична ступени Horus АКС Sänger за исключением меньших относительных размеров топливных баков и большего отсека полезной нагрузки (Таким образом, возникает французская концепция аппарата Radiance, о котором автор узнал на Московском аэрокосмическом салоне в сентябре 1993 г.). Однако давно известно, что комбинация ракетного двигателя и крыла далеко не оптимальна. Те, кому еще нужны дополнительные аргументы по этому вопросу, могут сравнить данные из п. 2, 3 для одноступенчатых крылатого и баллистического аппаратов. Более эффективной может быть баллистическая многоразовая вторая ступень типа аэрокосмического аппарата Delta Clipper, также совершающая вертикальную посадку с финальным гашением скорости при помощи двигателей.

Отношение массы конструкции носителя Delta Clipper к его стартовой массе составит 0.08 [25]. В соответствии со статистическими данными уменьшение масштаба аппарата с 450 - 500 т (Delta Clipper) до 100 т (характерная масса рассматриваемой второй ступени) в случае крылатых орбитальных аппаратов приводит к росту относительной массы конструкции примерно в 1.25 раза [15]. Принимая это соотношение и для баллистических носителей, получим, что относительная масса конструкции второй ступени АКС предлагаемой схемы на уровне технического совершенства носителя Delta Clipper составит 0.10. Если разместить вторую ступень на верхней поверхности первой в частично утопленном положении в аэродинамической тени, можно ограничить нагрузки и тепловые потоки, действующие на вторую ступень на траектории разгона величинами, не превышающими таковые при возвращении с орбиты.

Общие затраты топлива на маневры торможения на орбите и финального гашения скорости при вертикальной посадке оцениваются величиной 0.10 от посадочной массы второй ступени. Таким образом, если вторая ступень возвращается без полезной нагрузки, то масса этого топлива составит 0.01 от стартовой, если же возвращаемая нагрузка равна выводимой, то - 0.05. В итоге, масса выводимой на орбиту полезной нагрузки составит примерно 0.30 - 0.40 от стартовой, что в 5 - 10 раз выше, чем у второй ступени АКС типа Sänger. При этом относительная масса возвращаемой полезной нагрузки будет изменяться от 0.35 до 0.

Усложнение технических проблем в трех отмеченных выше ключевых комплексах гиперзвуковой технологии по сравнению с концепцией Sänger является ограниченным, причем, несколько уменьшая скорость разделения ступеней, можно, при необходимости, упрощать встающие перед конструкторами проблемы за счет некоторого уменьшения эффективности системы. Аэродинамический нагрев конструкции гиперзвукового летательного аппарата при кратковременном разгоне до чисел Маха 12 - 12.5 еще не вызывает непреодолимых трудностей при создании достаточно легкой авиационной конструкции [23], так как максимальные плотности тепловых потоков будут в 4 - 5 раз ниже, чем величины, указанные в п. 2 для одноступенчатого аэрокосмического самолета типа NASP [11].

Создание ГПВРД, эффективного при M = 6 - 12, не является проблемой слишком большого технического риска [8]. При использовании новых технических решений, упомянутых ниже и относящихся к схемам воздушно-реактивных двигателей для малых и умеренных скоростей полета (M ≤ 7), силовая установка первой ступени аэрокосмического самолета предлагаемой концепции, как и установка первой ступени АКС Sänger может состоять всего из двух модулей, а прямоточный воздушно-реактивный двигатель может быть использован только на режиме сверхзвукового горения, что серьезно упрощает его конструкцию и повышает эффективность его работы при M = 10 - 12.

Исключение таких элементов как крыло и вертикальное оперение второй ступени, а также ее простая геометрическая форма, близкая к конусу или оживальному телу [25], позволит создать интегрированную компоновку с частичным утапливанием второй ступени. Это даст возможность существенно приблизить максимальное аэродинамическое качество АКС на участках разгона и совместного крейсерского полета к величине K_max первой ступени, важность чего будет ясна из дальнейших оценок. Использование на второй ступени ракетного двигателя типа Aerospike кроме некоторого дополнительного увеличения его удельного импульса [27] поможет уменьшить донное сопротивление второй ступени.

5. Элементарная математическая модель летных данных первой ступени
аэрокосмического самолета (АКС)

Для более полной оценки предлагаемой концепции двухступенчатого аэрокосмического самолета необходимо определить также основные характеристики его первой ступени, к которым относятся (при фиксированных скорости и высоте разделения ступеней): отношение массы второй ступени к массе первой m₂/m₁, коэффициент заправочной массы f и радиус полета АКС от старта до момента разделения ступеней, и сравнить их с характеристиками АКС типа Sänger.

В первом приближении примем упрощенную модель полета первой ступени, состоящего из 5 основных участков, лежащих в одной плоскости: взлет (1), первый разгон (2), крейсерский полет (3), второй разгон (4) и, наконец, крейсерский полет - возвращение (5). Длиной участков взлета и снижения, а также влиянием переходов между основными режимами полета на его полную дальность пренебрегаем.

В используемой упрощенной модели полета сумма длин участков 2 - 4 равна длине участка 5. В конце второго разгона вследствие отделения второй ступени масса аэрокосмического самолета скачком уменьшается. Увеличением энергии в процессе взлета пренебрегаем и предполагаем, что АКС типа Sänger разгоняется от M = 0 до M = 4.5, крейсерский полет он выполняет при M = 4.5, далее разгоняется до M = 7.0 и возвращается при M = 4.5. Аэрокосмический самолет предлагаемой концепции первоначально разгоняется до M = 8.0, крейсерский полет совершает при этом же числе Маха, затем разгоняется до M = 12.5, а его возвращение происходит при M = 8.0.

Как обычно, будем полагать, что на участке взлета расходуется 1 % топлива от стартовой массы АКС. Кроме того, в модели первого приближения примем величину резерва топлива, равную 2 % от стартовой массы первой ступени аэрокосмического самолета (Δf = 0.02). В дальнейшем все индексы (a) относятся к параметрам разгона, а (с) - крейсерского полета.

Для того чтобы при заданных значениях радиуса полета АКС связать отношение масс первой и второй ступеней с коэффициентом заправочной массы первой ступени f = m_F/m₁, известны все необходимые приближенные выражения, кроме одного. Параметр f на участках разгона определяется из выражения (2.1). Дальность полета на крейсерских участках L_c вычисляется с помощью формулы Бреге [28], которую предпочтительно записать в следующей форме:

L_c = R_cln(z)/(1 - V_c²/V_E²), (5.1)

где R_c = η_cQK_c/g, η_c и K_c - соответственно пропульсивный коэффициент полезного действия и аэродинамическое качество на крейсерском режиме полета, V_c - крейсерская скорость полета, V_E - орбитальная скорость.

Примем, как обычно, в первом приближении K_c = K_max, последний член в выражении (5.1), учитывающий кривизну траектории, обозначим

ξ_c ≈ (1 - M_c²/M_E²)^-1, (5.2)

где M_E = 25. Отношение масс в конце m_i+1 и в начале m_i каждого участка выражается следующим образом:

m_i+1/m_i = 1/z. (5.3)

Соотношение (3.2) связывает z и f. Чтобы замкнуть систему уравнений, необходимо найти приближенное соотношение между z или f и длиной траектории на участке разгона.

На пологих участках траектории в скоростной системе координат уравнения движения с точностью до O(θ²) имеют следующую форму:

m(dV/dt) = P - (X + Gθ),	(5.4)
Y = nξG,	(5.5)
dL/dt = V,	(5.6)

где t - время, Y - подъемная сила, G - вес аппарата, n = Y/mg - нормальная перегрузка, θ - угол наклона траектории.

Как и ранее под θ будем понимать среднюю на данном участке траектории величину. Если обозначить δ = Kθ/nξ, где K - аэродинамическое качество, из (5.4 - 5.5) следует, что

X + Gθ = X(1 + δ). (5.7)

В дальнейшем будет показано, что для предварительной оценки распределения коэффициента заправочной массы f по участкам полета первой ступени аэрокосмического самолета, а также для определения радиуса его полета, величинами порядка δ можно пренебречь. В таком случае, как и при выводе выражения (2.1), для средней по участку траектории величины отношения тяги к сопротивлению P/X = φ + 1 и для среднего значения нормальной перегрузки n, в квазистационарном приближении легко получить соотношение:

L = R ln(z)/[n(φ + 1)], (5.8)

где R = ηQK/g, η и K - соответственно средние пропульсивный коэффициент полезного действия и аэродинамическое качество на данном участке траектории.

Обозначим через ω отношение среднего коэффициента подъемной силы на рассматриваемом участке полета к величине Cy_opt = Cy(K_max), где K_max - максимальное аэродинамическое качество: ω = Cy/Cy_opt. Поляры гиперзвуковых летательных аппаратов, по крайней мере, при M ≤ 10 и коэффициенте подъемной силы Cy не превышающем существенно Cy_opt, с точностью 2 - 3 % аппроксимируются квадратичными зависимостями. Эту аппроксимацию удобно представить следующим образом [29]:

Cx = Cx₀ + Cy²/A -(±BCy) (Cy ≥ 0), (5.9)

где знак минус соответствует прямому положению компоновки, а знак плюс - перевернутому. Линейный по Cy член описывает асимметрию поляры относительно оси Cx. Используется и упрощенное выражение:

Cx = Cx₀ + Cy²/A. (5.10)

Из формулы (5.10) следует, что

K/K_max = 2ω/(1 + ω²). (5.11)

Если через K₀ обозначить величину K_max из выражения (5.10), то

K_max = K₀/[1 -(±BK₀)] = K₀[1 ± BK₀ + o(BK₀)], (5.12)

где

K₀ = 0.5(A/Cx₀)^0.5.

Погрешности определения K_max по формуле (5.10) по сравнению с более точным выражением (5.9) в отдельных случаях могут превысить 10 %, однако погрешность выражения (5.11), как легко показать, составляет

±BK₀(1 - ω)²/(1 + ω²) + o[BK₀(1 - ω)²/(1 + ω²)],

и в интересующем нас диапазоне изменения ω ≥ 0.4 не превышает 2 - 3 %. Для наиболее асимметричной поляры, известной автору, и относящейся к описанной в п. 7 компоновке при M = 9.8 BK₀ = 12.5 %, а погрешность формулы (5.11) при ω = 0.5 составляет всего 1.1 %.

Тогда из выражений (5.8) и (5.11) следует аналог формулы Бреге для любого пологого участка траектории полета аэрокосмического самолета:

L = 2ωR_mln(z)/[n(1 + ω²)(φ + 1)], (5.13)

где R_m = ηQK_max/g.

Если Y = G, n = 1/ξ, и при пологом разгоне аппарата

L_a = 2ωξR_mln(z)/[(1 + ω²)(φ + 1)]. (5.14)

При этом, если вернуться к выражению (5.7),

δ = 2ωθK_max/[nξ(1 + ω²)], (5.15)

определяющему погрешность от пренебрежения проекцией веса на направление касательной к траектории, то при характерных параметрах, полученных из последующих расчетов, в определение длины первого разгонного участка может быть внесена ошибка до 20 %, а на втором разгонном участке ошибка составит 2 - 3 %.

Однако, изменение длины крейсерского участка траектории на некоторую величину требует в 3 - 4 раза меньше затрат топлива, чем такое же изменение длины участка траектории на разгоне. Вдобавок, чем больше погрешность (5.15), тем меньше длина участка разгона, и тем меньшую долю она составляет от полной длины траектории, так что влияние фактора (5.15) на длину траектории невелико.

После того, как по описанной выше модели первого приближения получена связь между скоростью и дальностью полета, при известной зависимости между скоростью и высотой полета можно учесть влияние проекции веса на направление касательной к траектории и ввести эффективное сопротивление:

X_* = X(1 + δ). (5.16)

Далее можно повторить всю процедуру расчета, определяя параметр φ следующим образом:

φ = P/X_* - 1, (5.17)

построив, таким образом, модель второго приближения оценки летных данных первой ступени аэрокосмического самолета.

Таким образом, выражения (2.1), (3.2), (5.1), (5.3) и (5.14) - (5.17) составляют замкнутую систему соотношений для средних значений летных данных аэрокосмического самолета, позволяющую оценить важнейшие характеристики его первой ступени в случае плоского выведения полезной нагрузки на орбиту. При необходимости, на основе этих формул можно построить итерационный процесс для уточнения длин участков разгонов или расхода топлива. Разбивая каждый участок на достаточно малые части при известных характеристиках двигателя и аэродинамике легко создать быстрый численно-аналитический метод расчета летных данных при разгоне и крейсерском полете для летательных аппаратов с малыми и умеренными значениями аэродинамического качества и большой тяговооруженностью.

6. Сравнительный анализ основных характеристик первых ступеней АКС классической и альтернативной схем при плоском выведении полезных нагрузок на орбиту

Построенная в п. 5 работы элементарная математическая модель позволяет оценить в первом приближении основные летные данные первой ступени аэрокосмического самолета. Желательно проверить ее работоспособность на уже отработанной в известной степени ступени АКС типа Sänger. Кроме того, используя не абсолютные, а отнесенные к характеристикам этого аппарата параметры, можно добиться большей точности оценки гиперзвуковых самолетов новых схем. Однако ни характеристики постоянно изменяющейся силовой установки АКС Sänger [21,22], ни даже величина максимального аэродинамического качества на крейсерском режиме полета автору данной работы не известны. Сообщается только, что для компоновки из двух ступеней величина K_max находится между 4 и 5, а для отдельной первой ступени - между 5 и 6 [21].

Известно, что за 1987 - 1991 годы отношение масс первой и второй ступеней m₁/m₂ у АКС Sänger изменилось от 2.66 до 2.27 [21,22], коэффициент заправочной массы уменьшился со значения f = 0.42 до f = 0.39 [21,22], а радиус полета R₀ сократился от 3500 км до 3000 км [21,30]. Примем в качестве исходных несколько округленные величины 1991 года: m₁/m₂ = 2.25, f = 0.40 и R₀ = 3000 км. Если массу топлива первой ступени отнести к стартовой массе всего аэрокосмического самолета, то соответствующий коэффициент заправочной массы будет равен f₀ = m_F/(m₁ + m₂) = 0.28. Приблизительно известны и основные параметры траектории разгона [21].

По данным работ [8,31] с использованием соотношения

η = IV/Q, (6.1)

где I - удельный импульс силовой установки, была построена типовая зависимость величины пропульсивного коэффициента полезного действия η от числа Маха полета M (рис. 2) для аэрокосмических самолетов рассматриваемых типов. При M = 0.5 удельный импульс составляет величину I = 7·10⁴ м/с, при M = 4.5 - I = 3.9·10⁴ м/с. Когда M > 12, неопределенность характеристик ГПВРД катастрофически возрастает, приводя к значительной неопределенности характеристик АКС с воздушно-реактивными двигателями, максимальное число Маха полета которого значительно больше 12. В дальнейших расчетах при M = 12.5 величина η соответствует I = 1.44·10⁴ м/с.

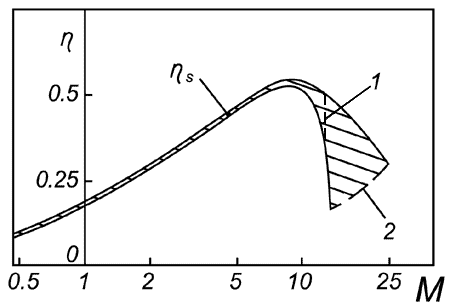Рис. 2

Линия 1 на рис.2 построена при M = 12.5, кривая 2 - для значений пропульсивного коэффициента полезного действия ГПВРД таких, что его удельный импульс равен удельному импульсу водородно-кислородного ракетного двигателя в вакууме (I = 4.7·10³ м/с). Отметим, что среднее значение η = 0.4 для силовой установки аэрокосмического самолета типа NASP, которое было принято в п. 2 вслед за работой [14], соответствует практически не достижимой верхней границе зоны η(M).

Введем параметр k, характеризующий индивидуальные отклонения различных силовых установок от типовой кривой η(M). Для АКС Sänger на крейсерском режиме примем k_S = 1. Все длины полета отнесем к некоторой характерной длине L₀. Поделив в формуле (5.1) обе ее части на L₀, получим на режиме крейсерского полета АКС типа Sänger безразмерный параметр σ_S = (ξ_Sk_Sη_SQK_S)/(gL₀), где индекс (S) обозначает параметры этого АКС вместе со второй ступенью на крейсерском режиме, а ξ_S - определяется из формулы (5.2) на этом же режиме. Введем параметры p₁, p₂, p₃, p₄, p₅, где p₁ = k/k_S, p₂ = K_max/K_S, p₃ = η/η_S, p₄ = ξ/ξ_S, p₅ = 1 для участков крейсерского полета и p₅ = 2ω/[(1 + ω²)(φ + 1)] для участков разгона. Тогда формулы (5.1) и (5.14) нормируются для безразмерной длины полета l = L/L₀ на любом участке траектории плоского выведения:

l = p₁p₂p₃p₄p₅σ_Sln(z). (6.2)

Анализ аэродинамических характеристик типичных гиперзвуковых компоновок показал, что при скоростных напорах на участках разгона 60 - 70 кПа и начальной нагрузке на крыло G₀/S = 3 - 3.5 кПа, характерная величина ω_a = Cy_a/Cy_c = 0.5 (ω_a ≈ q_c/q_a). Параметрические исследования среднего отношения тяги к сопротивлению P/X = φ + 1 по формуле (2.1) привели к выбору для АКС Sänger φ = 1.0 (M_max = 7) и для аэрокосмического самолета альтернативной схемы - φ = 1.5 (M_max = 12.5). Напомним, что в соответствии с работой [14] у АКС типа NASP φ = 2.5 (M_max = 25). Следовательно, для немецкой концепции на участках разгона p₅ = 0.40, для альтернативной - p₅ = 0.32. Средние значения параметров p₃ и p₄ легко вычисляются. Оценки параметров p₁ и p₂ для аппарата типа Sänger на участках траектории 2 - 5 приведены в следующей таблице 1:

N	2	3	4	5
p₁	1.0	1.0	1.0	1.0
p₂	1.0	1.0	0.9	1.2

По-видимому, оценки значений параметра p₁ довольно оптимистичны, и при получении дополнительной информации их можно будет уточнить. Максимальное аэродинамическое качество гиперзвуковых компоновок при M = 2 - 4.5 обычно изменяется незначительно, а при меньших числах Маха в процессе разгона набирается только около четверти энергии. На трансзвуковом режиме полета происходят наиболее сложные явления, приводящие в целом к увеличению затрат топлива, прямо учесть которые в этой элементарной модели не представляется возможным. Поэтому, для косвенного учета ухудшения разгонных характеристик при трансзвуковых скоростях не принимается во внимание увеличение там уровня максимального аэродинамического качества, и для параметра p₂ на участке первого разгона (2) принята величина 1.0. Оценить среднее уменьшение K_max с ростом числа Маха на участке второго разгона (4) можно по соотношению Кюхемана [28]:

K_max ~ (M + 3)/M. (6.3)

Оценка увеличения максимального аэродинамического качества на режиме крейсерского полета после отделения второй ступени дает значение параметра p₂ = 1.2 для участка 5.

Из соотношений (2.1), (3.2), (5.3), (6.2) и

l₂ + l₃ + l₄ = l₅ = 0.5 (l₁ = 0) (6.4)

при f = 0.40 итерационным путем можно определить значение безразмерной константы σ_S = 3.45. При этом можно построить зависимость коэффициента заправочной массы f АКС Sänger от числа Маха полета M (рис. 3, ломаная линия S). Пунктиром обозначены участки торможения, не требующие затраты топлива.

Примем, что радиус полета R₀ рассматриваемых аэрокосмических самолетов составляет 0.4 от номинальной дистанции полета L₀. В п. 10 работы будет показано, как при пространственном выведении на орбиту полезных нагрузок построить траектории, удовлетворяющие этому условию. Тогда, при номинальном радиусе полета АКС Sänger R₀ = 3000 км, номинальная дистанция полета составит L₀ = 7500 км, максимальное аэродинамическое качество АКС Sänger на крейсерском режиме вместе со второй ступенью оценивается величиной K_max = 4.6, а без нее - K_max = 5.5.

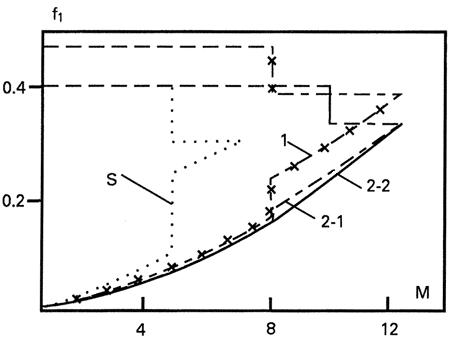Рис. 3 - Расход топлива в случае плоского выведения

Оценки параметров p₁ и p₂ для аппарата альтернативной схемы, использующего традиционные решения в аэродинамике и конструкции силовой установки (АКС-1), для участков траектории 2 - 5 приведены в таблице 2:

N	2	3	4	5
p₁	1.0	1.0	0.975	1.0
p₂	1.0	0.9	0.85	0.95

Предполагается, что значения пропульсивного коэффициента полезного действия двигателей АКС-1 также лежат на стандартной кривой, показанной на рис. 2, за исключением больших чисел Маха полета. Вследствие того, что на АКС-1 должен применяться двухрежимный ПВРД, использующий как дозвуковое, так и сверхзвуковое горение (см. п. 2), значение параметра p₁ на максимальной скорости на втором участке разгона принято на 5 % ниже, чем при M = 8, что и дает указанную в таблице 2 среднюю величину p₁ на втором участке разгона.

Среднее уменьшение K_max вследствие роста числа Маха полета АКС-1 оценивается по формуле (6.3), однако принимается во внимание, что частичное утапливание бескрылой второй ступени уменьшает максимальное аэродинамическое качество комбинации двух ступеней на 10 %, а наличие углубления на верхней поверхности первой ступени - соответственно на 5 % по сравнению с чистыми ее формами. Таким образом, при M = 8 для АКС-1 K_max = 4.1 при совместном полете двух ступеней.

Зависимость коэффициента заправочной массы f от числа Маха полета M для АКС-1 (m₁/m₂ = 2.25) показана на рис. 3 ломаной линией 1. Увеличение затрат топлива в 2 раза при разгоне по сравнению с АКС типа Sänger при возрастании длины дистанции разгона в 2.2 раза (следует помнить, что в рамках используемой модели первого приближения общая длина участков разгона определяется с точностью не выше 5 - 10 %), привело к тому, что несмотря на сокращение суммарной длины крейсерских участков от 0.87 до 0.72 от полной дистанции полета и снижение затрат топлива при этом в 1.6 раза по сравнению с аппаратом типа Sänger, при сохранении заданной дальности полета необходимый коэффициент заправочной массы f возрос с 0.40 до 0.47. Следовательно, величина параметра f АКС-1 должна принимать промежуточные значения между соответствующими величинами аэрокосмических самолетов типа Sänger и типа NASP. Такое увеличение коэффициента заправочной массы соответствует росту в 1.35 раза отношения массы топлива, размещаемого на первой ступени АКС, к массе ее конструкции, что является чрезвычайно трудной, а может быть и невыполнимой задачей при создании рассматриваемых двухступенчатых систем в предвидимом будущем.

Оценки показывают, что при сохранении радиуса действия и коэффициента заправочной массы f = 0.40, стартовая масса первой ступени АКС-1 должна относиться к стартовой массе второй ступени как 6.50 : 1. При этом относительная масса полезной нагрузки АКС-1 составит около 4.5 % (Для аппарата типа Radiance с крылатой верхней ступенью этот показатель будет около 3 %), что не слишком превосходит максимальные значения для аэрокосмического самолета типа Sänger (2.5 %), и в таком исполнении альтернативная схема АКС не является чрезмерно привлекательной. Однако, использование уже найденных новых фундаментальных решений в схемах воздушно-реактивных двигателей и, особенно, в гиперзвуковой аэродинамике, приводит к кардинальному изменению этой оценки.

7. Интерференционная концепция аэродинамического проектирования гиперзвуковых летательных аппаратов

Несмотря на то, что 3/4 топлива АКС-1 при f = 0.47 расходуется на участках разгона, важнейшим фактором, определяющим основные характеристики космической транспортной системы при фиксированной дальности полета для обеспечения необходимого параллакса орбиты полезной нагрузки, как будет видно из п. 9, 10, является максимальное аэродинамическое качество K_max при гиперзвуковых скоростях полета. Увеличение этого параметра, особенно при выполнении различных конструктивных ограничений, когда следует сохранить объем и массу авиационной конструкции, является одной из наиболее сложных проблем аэродинамики.

Численные исследования в рамках предложенной автором интерференционной концепции аэродинамического проектирования гиперзвуковых летательных аппаратов (некоторые результаты опубликованы в работах [29,32,33]) позволили проанализировать влияние геометрии и режима обтекания на интерференцию крыла и корпуса при гиперзвуковых скоростях полета и найти способы более эффективного формирования и использования возмущенного за головной ударной волной поля течения путем ограниченных изменений геометрии компоновки и введения небольших дополнительных элементов, что приводит к существенным отличиям во взаимодействии компоновки с набегающим потоком, и, соответственно, - к значительному росту величины максимального аэродинамического качества K_max при гиперзвуковых скоростях полета.

При больших числах Маха эти конфигурации обладают существенно бóльшими значениями K_max, чем известные комбинации крыла и корпуса. С ростом числа Маха уровень их аэродинамического качества практически не уменьшается. При малых и умеренных сверхзвуковых скоростях полета аэродинамические характеристики предлагаемых конфигураций мало отличаются от характеристик типичных комбинаций корпуса с крылом малого удлинения. На малых скоростях полета их несущие способности близки к характеристикам традиционных гиперзвуковых компоновок. Конструкция разработанных компоновок мало отличается от конструкции классических комбинаций крыла и корпуса.

Испытания в аэродинамической трубе модели, спроектированной на основании этих принципов, продемонстрировали при М = 7 - 10, числах Рейнольдса (5 - 8)·10⁶ и коэффициенте объема модели τ = ν^2/3/S = 0.21, где ν - объем корпуса, а S - площадь крыла конфигурации, что близко к величине коэффициента τ АКС Sänger, уровень K_max = 5.75 - 5.6 (см. кривую 2 на рис. 4). В зависимости от числа Маха это на 15 - 30 % выше, чем у известных компоновок (штриховая область 1 на рис. 4). При M = 7 и 9.8 на кривой 2 нанесены отметки, характеризующие среднеквадратичное отклонение величины K_max по результатам соответственно трех и пяти испытаний.

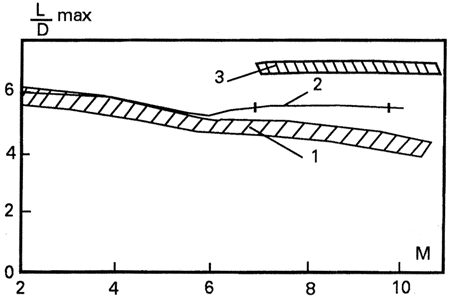Рис.4 - Уровни максимального аэродинамического качества

Пересчет на натурные числа Рейнольдса, характерные для траекторий аэрокосмических самолетов (Re ~ 10⁸ по длине аппарата при M = 7 - 12), а также прямые эксперименты в ударной аэродинамической трубе [34], демонстрируют увеличение K_max в 1.2 раза по сравнению с приведенными на кривых 1 и 2 рис. 4 уровнями максимального аэродинамического качества. Оптимизация крутки крыла дополнительно увеличивает K_max приблизительно еще на 0.2 [33]. Таким образом, натурный уровень K_max предлагаемых гиперзвуковых компоновок при M = 7 - 12 будет K_max = 6.9 - 7.1 (штриховая область 3 на рис. 4). Кроме того, конфигурации такого типа могут лучше экранировать при больших скоростях полета объекты, расположенные на их верхних поверхностях.

Установка хорошо спроектированной мотогондолы и вертикального оперения уменьшит уровень максимального аэродинамического качества первой ступени АКС с 7.0 не более чем до 6.5. Принимая сбалансированные величины K_max новой компоновки аэрокосмического самолета альтернативной схемы, названного АКС-2, равными 6.0 без второй ступени и 5.7 - 5.75 в полной сборке, мы используем консервативные оценки, которые, без сомнения, могут быть превышены. Таким образом, на участках гиперзвукового разгона и крейсерского полета АКС-2 мы практически возвращаемся к трубным значениям K_max при некотором перераспределении сопротивлений трения и волнового. При большем утапливании и/или тщательной отработке взаимной интерференции ступеней, можно ожидать уровни максимального аэродинамического качества при гиперзвуковых скоростях на 5 - 10 % выше, чем те, которые используются в дальнейших расчетах.

Следует отметить, что по экспериментальным данным при M = 10 (а здесь практически наступает гиперзвуковая стабилизация) и уровнях скоростного напора и удельной нагрузки на крыло, указанных в п. 6, с учетом уменьшения массы АКС из-за выгорания топлива и влияния кривизны траектории (формула (5.2)), на траектории разгона подъемная сила при M = 10 - 12 вдвое превосходит вес аппарата при Cy = Cy_opt. Это позволит провести достаточно эффективный и экономичный маневр увеличения угла тангажа траектории перед разделением ступеней.

В России описываемые конфигурации признаны изобретением. Применение их позволит, как будет видно из п. 9, резко улучшить основные характеристики двухступенчатого аэрокосмического самолета предлагаемой схемы.

8. Концепция воздушно-реактивного двигателя для гиперзвуковых летательных аппаратов

Комбинированные силовые установки, которые необходимо использовать на аэрокосмических самолетах, при удовлетворительных уровнях их удельных импульса и тяги, отличаются сложностью переменной геометрии их внутренних трактов, большими поперечными габаритами, приводящими к росту аэродинамического сопротивления, и значительной массой [35]. Все это существенно затрудняет создание действительно эффективных АКС. Чрезвычайно желательным было бы создание воздушно-реактивного двигателя, способного достаточно эффективно работать во всем диапазоне чисел Маха полета, в котором еще можно затормозить поток газа без получения чрезмерно высоких температур и давлений торможения, то есть при M ≤ 6.5 - 7.

В этом случае первая ступень АКС типа Sänger и любые гиперзвуковые аппараты с предельным числом Маха полета менее 7 могли бы иметь силовую установку, состоящую не из двух, а из одного типа двигателя. Проблемы силовой установки предлагаемого двухступенчатого аэрокосмического самолета альтернативной концепции, как уже говорилось выше, также существенно бы упростились. В частности, прямоточный воздушно-реактивный двигатель АКС мог бы работать только в режиме сверхзвукового горения, что уменьшило бы его сложность и массу и увеличило бы его удельный импульс на верхней границе скорости разгона.

Уникальные физико-химические свойства топлива этих аппаратов - жидкого водорода стимулируют поиски новых схем воздушно-реактивных двигателей, более адекватно удовлетворяющих предъявляемым к ним противоречивым требованиям на всем рабочем участке траектории. Интересной попыткой такого рода является двигатель инверсного цикла (I.C.E. ONERA, [20]), способный работать в непрерывном режиме при числах Маха от M = 0 до M = 6 - 7. Однако все его положительные качества обесцениваются тем, что это возможно только при расходах топлива в 2 - 2.5 раза превышающих стехиометрический, то есть соответствующий полному использованию в процессе горения кислорода воздуха [35]. Это обстоятельство связано с противоречивыми требованиями, предъявляемыми обратным циклом Брайтона (Джоуля) к теплоте сгорания и хладоресурсу жидкого водорода.

Исследования показывают, что дальнейшее развитие схемы инверсного воздушно-реактивного двигателя, использующее идеи, обычно применяемые при разработке некоторых типов турбокомпрессорных двигателей для гиперзвуковых летательных аппаратов, позволяет разрешить указанное выше противоречие. Предварительные оценки позволяют утверждать, что двигатель предлагаемой новой схемы во всем диапазоне чисел Маха от М = 0 до М = 6 - 7 может работать в непрерывном режиме при расходе топлива близком или даже меньшем, чем стехиометрический, и на малых скоростях полета его удельные импульс и тяга могут быть близки к соответствующим характеристикам турбореактивного двигателя с форсажной камерой, а с ростом скорости полета вплоть до предельной его характеристики становятся на 15 - 20 % выше, чем у любого известного типа воздушно-реактивного двигателя.

В сочетании со значительно бóльшим диапазоном рабочих скоростей полета, чем у известных турбокомпрессорных двигателей, а также сравнительно низкими температурами газового потока во всем турбокомпрессорном тракте, это делает предлагаемую концепцию силовой установки чрезвычайно привлекательной для применения на гиперзвуковых летательных аппаратах. При этом двигатель, как правило, сможет заменить комбинацию из двух прежних типов двигателей.

В России схема предлагаемого воздушно-реактивного двигателя признана изобретением. Его применение также позволит улучшить характеристики рассматриваемого двухступенчатого аэрокосмического самолета.

9. Влияние предлагаемых инноваций на основные характеристики АКС рассматриваемой схемы

Оценки параметров p₁ и p₂ для аппарата альтернативной схемы, использующего инновационные решения в аэродинамике и конструкции силовой установки (АКС-2), для участков траектории 2 - 5 приведены в таблице 3:

N	2	3	4	5
p₁	1.1	1.0	1.025	1.0
p₂	1.1	1.25	1.25	1.3

Предполагается, что на участке первого разгона до M = 6 - 6.5 работает турбокомпрессорный двигатель, кратко описанный в п. 8 работы, а далее на всех остальных участках полета действует ГПВРД в режиме сверхзвукового горения. С учетом сказанного в п. 8, средний коэффициент полезного действия силовой установки АКС-2 на участке первого разгона (2) принят на 10 % больше (p₁ = 1.1), чем у АКС-1. На участках крейсерского полета (3) и (5) различий в величинах параметра p₁ нет, а при втором разгоне (4) p₁ больше на 5 %, так как однорежимный ГПВРД будет иметь при больших числах Маха лучшие характеристики, чем более сложный двухрежимный ПВРД.

Значения параметра p₂ на участках полета (3) - (5) получаются делением величин K_max для новой компоновки из п. 7 на K_S = 4.6. Оценка величины параметра p₂ при первом разгоне (2) - осреднение ее максимального аэродинамического качества по отношению к лучшим компоновкам традиционного типа в диапазоне M = 0.5 - 8.0 (см. рис. 4) с учетом того, что при M < 2 набирается не более 11 % энергии. Аэродинамические характеристики АКС-2 позволяют ему, вследствие значительного уменьшения веса после разделения ступеней, совершать крейсерский полет - возвращение (5) при M = 10, что также несколько улучшает его основные характеристики.

Зависимость коэффициента заправочной массы f от числа Маха полета M для описанного выше АКС-2-1 показана на рис. 3 ломаной линией 2-1. Улучшение характеристик силовой установки АКС-2-1 приводит к уменьшению затрат топлива в 1.05 раза при разгоне по сравнению с АКС-1. Однако, что существенно более важно, рост аэродинамического качества при разгоне увеличивает длину разгонной дистанции в 1.35 раза. Это дает сокращение суммарной длины крейсерских участков от 0.72 для АКС-1 до 0.62 от полной дистанции полета, причем, естественно, все сокращение приходится на участок (3) полета с большой полезной нагрузкой и еще значительным запасом топлива. На прямом этапе полета АКС-2-1 длина крейсерского участка составляет не более 1/4 дальности. Вместе со значительным увеличением K_max на крейсерском режиме все это вызывает уменьшение расхода топлива на участках полета (3) и (5) в 1.7 раза по сравнению с АКС-1. В итоге, при m₁/m₂ = 2.25 коэффициент заправочной массы f АКС-2-1 равен 0.40, что совпадает с величиной этого параметра АКС Sänger.

Таким образом, предлагаемая альтернативная схема двухступенчатого аэрокосмического самолета при умеренном техническом риске позволяет, по предварительным оценкам, выводить на низкую околоземную орбиту полезные нагрузки, составляющие 9 - 12 % от его стартовой массы при радиусе полета на параллакс R₀ = 3000 км.

Однако реальные траектории аэрокосмических самолетов в пространстве значительно отличаются от исследованных траекторий плоского выведения. Дополнительные затраты топлива по сравнению с рассмотренными выше полетными сценариями могут быть вызваны такими необходимыми для выполнения задачи полета маневрами как кабрирование при разделении ступеней и, особенно, разворотами на больших гиперзвуковых скоростях для выхода АКС на курс запуска второй ступени и для возвращения первой ступени в точку старта.

Рассмотренные модели траекторий в целом соответствуют схеме полета АКС Sänger. Рост максимального числа Маха в 1.8 раза увеличивает удельную энергию аппарата в 3.2 раза, поэтому следует ожидать, что для аэрокосмических самолетов предлагаемого типа более выгодными могут быть качественно иные траектории.

Рассмотрим АКС-2-2, аэродинамические характеристики и эффективность силовой установки которого не отличаются от соответствующих параметров АКС-2-1. Однако разгон нового варианта аэрокосмического самолета будем осуществлять по иному сценарию. Кроме того, учтем планирование аппарата при возвращении. Все топливо, расходуемое АКС-2-1 на двух участках интенсивного разгона (2) и (4) и крейсерского полета (3) затратим на менее интенсивный и более длинный разгон. До M = 6.5 на участке работы турбокомпрессорного двигателя все остается по-прежнему (φ = 1.5, ω = 0.5), а при M = 6.5 - 12.5, как показывает соответствующая итерационная процедура, в которой используются выражения (2.1), (3.2), (5.3) и (6.2), при заданном запасе топлива необходимое приращение энергии достигается на разгоне с параметрами φ = 1.1, ω = 0.7. Дальность полета АКС-2-2 от старта до достижения точки разделения ступеней при M = 12.5 увеличивается при этом на 10 % по сравнению с дальностью АКС-2-1.

Значительная удельная энергия первой ступени АКС-2 при M = 12.5 и ее высокое максимальное аэродинамическое качество определяют большую дальность планирования этого аппарата. Легко получить приближенное выражение:

l_g = ξK_maxΔE/gL₀, (9.1)

где l_g = L_g/L₀ - относительная дальность планирования, в качестве ξ и K_max, как и ранее, принимаются средние на участке планирования величины, а ΔE - изменение в процессе планирования удельной энергии аппарата.

Планирование происходит при уменьшении числа Маха от 12.5 до 10, затем, как и ранее, следует участок крейсерского полета при M = 10, длина которого такая же, как у АКС-2-1, и, наконец, - заключительное планирование от М = 10 до М = 0.8. Условие равенства дистанций полета от старта до разделения ступеней и обратного (6.4) в данном случае снимается. В итоге, полная дальность полета АКС-2-2 по рассмотренной траектории составит l = 1.80, причем более 41 % этой дистанции приходится на участки планирования. Зависимость коэффициента заправочной массы f от числа Маха полета M для АКС-2-2 показана на рис. 3 ломаной линией 2-2.

Таким образом, у аэрокосмического самолета предлагаемой схемы есть значительные резервы по сравнению с проведенными выше оценками, и эти резервы можно использовать для выполнения необходимых маневров в реальном полете в трехмерном пространстве.

10. Сравнительный анализ основных характеристик первых ступеней АКС классической и альтернативной схем при пространственном выведении полезных нагрузок на орбиту

Для анализа основных характеристик первых ступеней аэрокосмических самолетов при пространственном выведении полезных нагрузок на околоземную орбиту необходимо оценить затраты энергии на развороты. Учтем также и затраты энергии на кабрирование АКС перед разделением ступеней. Используя и далее метод осреднения параметров рассматриваемых процессов и полагая, что радиус кривизны траектории на вираже остается постоянным вследствие изменения крена аппарата, легко получить выражение для оценки длины участка траектории на вираже, являющейся в этом приближении частью окружности:

l_t = ξV²ψ/[gL₀(n²ξ² - 1)^0.5], (10.1)

где l_t = L_t/L₀ - относительная длина траектории виража, а ψ - угол разворота на вираже. Относительный радиус виража равен:

r_t = l_tψ^-1. (10.2)

После разделения ступеней целесообразно уменьшить на вираже скорость полета до крейсерской, при этом разворот можно осуществлять с выключенными двигателями за счет накопленной ранее энергии. Пренебрегая изменением высоты полета (потенциальная энергия АКС при M = 12.5 составляет около 5 % от кинетической), нетрудно вывести приближенное соотношение, связывающее снижение скорости на вираже с углом разворота:

V₁/V₀ = 1/exp{nξψ/[K_t(n²ξ² - 1)^0.5]}, (10.3)

где V₀ и V₁ - соответственно начальная и конечная скорости при развороте с торможением, K_t - среднее аэродинамическое качество, при котором совершается этот разворот.

Относительная длина участка траектории l_p = L_p/L₀, на котором выполняется маневр кабрирования на заданный угол e, в рамках тех же приближений оценивается следующим образом:

l_p = ξV²ε/[gL₀(nξ - 1)]. (10.4)

Соотношения (3.2), (5.3), (6.2) (параметр p₄ в этом случае должен определяться как p₄ = n_S/n) вместе с выражениями (10.1) или (10.4) позволяют оценить расходы топлива на маневры разворота при пространственном выведении полезной нагрузки и кабрирования для разделения ступеней, а соотношение (10.3) - число Маха полета при выходе из виража с торможением.

Используя полученные соотношения, рассмотрим траектории двухступенчатых АКС классической и альтернативной схем в пространственном случае при полете на параллакс. В соответствии с работой [15] к рассмотренным в п. 6 пяти участкам полета АКС типа Sänger добавляются еще четыре. После первого разгона и крейсерского полета на юг, длина которого составляет около 3/4 от того, что было при плоском выведении, на крейсерском числе Маха M = 4.5 и при максимальном аэродинамическом качестве выполняется разворот на восток (см. кривую S на рис. 5) с перегрузкой n = 1.07 (nξ = 1.1), так что при его завершении достигается удаление на юг от точки старта r₀ = 0.4. Затем происходит второй разгон до M = 7 при полете в восточном направлении, аналогичный рассмотренному в п. 6, короткий участок кабрирования (ε = 0.1 ~ 6°, [15]), разделение ступеней и вираж на 110° с максимальной перегрузкой n_max = 2.5 на режиме максимального аэродинамического качества K_t = K_max (см. рис. 5). При этом масса первой ступени на вираже составит не более 48 % от стартовой массы АКС, что позволяет создавать такие перегрузки при максимальном аэродинамическом качестве и ограничивает нагрузки на конструкцию первой ступени. После этого аэрокосмический самолет выходит на курс возвращения в точку старта, совершает крейсерский полет при M = 4.5 и завершающее планирование до M = 0.8, показанное на рис. 5, как и разворот с торможением, пунктиром. Полная длина полетной дистанции составит 0.96 от номинальной полетной длины L₀, причем около 0.11 приходится на полет без затрат топлива.

Зависимость коэффициента заправочной массы f от числа Маха полета M для АКС типа Sänger показана на рис. 6 ломаной линией S. Таким образом, при пространственном выведении полезной нагрузки на орбиту с удалением на юг точки старта второй ступени на расстояние 0.4 L₀ от точки взлета АКС, коэффициент f составит по проведенным оценочным расчетам величину f = 0.38, что на 0.02 меньше, чем в рассмотренной в п. 6 плоской модели полета, и всего на 0.01 меньше, чем величина f = 0.39, приводимая разработчиками АКС Sänger при том же радиусе полета R₀ = 3000 км и том же соотношении масс первой и второй ступени m₁/m₂ ≈ 2.25 [15,22] и показанная на рис. 6 точкой P_S.

Таким образом, можно констатировать хорошее согласование результатов первого приближения предложенной математической модели основных летных данных первой ступени АКС со всем комплексом сведений, опубликованных об аэрокосмическом самолете Sänger.

Траектория полета аэрокосмического самолета альтернативной схемы АКС-2-2 при пространственном выведении несколько более проста, чем у аппарата типа Sänger, так как состоит не из 9, а из 7 участков. Первоначально, как и в п. 9, происходит интенсивный разгон (φ = 1.5, ω = 0.5) на этапе работы турбокомпрессорного двигателя при числе Маха от 0 до 6.5. При этом АКС-2-2 движется на юг. С момента начала работы ГПВРД начинаются разгон и одновременно разворот на восток (см. кривую 2-2 на рис. 5) при φ = 0.97 и ω = 0.77, что обеспечивает необходимую для такого виража среднюю "перегрузку" n = 0.93 (nξ = 1.09) при максимальной перегрузке n_max ≈ 1.0. Количество топлива, расходуемое при этом маневре, примерно на 6 % больше, чем при плоском разгоне АКС-2-2 из п. 9, однако и длина полетной дистанции возрастает на такую же величину вследствие увеличения среднего аэродинамического качества и уменьшения отношения тяги к сопротивлению на этом участке полета, вызванных ростом параметра ω и уменьшением параметра φ, что обеспечивает в конце этого этапа не только необходимые скорость, высоту и направление полета на восток, но и смещение АКС к югу от точки старта на расстояние r₀ = 0.4 (см. рис. 5).

Далее следуют короткий этап кабрирования (ε = 0.1), разделение ступеней и вираж на 140° с максимальной перегрузкой n_max = 2.5 на режиме максимального аэродинамического качества K_t = K_max (см. рис. 5). При этом масса первой ступени на вираже составит не более 45 % от стартовой массы АКС. После этого аэрокосмический самолет выходит на курс возвращения в точку старта, совершает крейсерский полет при M = 8.5 и завершающее планирование до M = 0.8, показанное на кривой 2-2 рис. 5, как и разворот с торможением, пунктиром. Полная длина полетной дистанции составит 1.24 от номинальной полетной длины L₀, причем около 0.44 приходится на полет без затрат топлива.

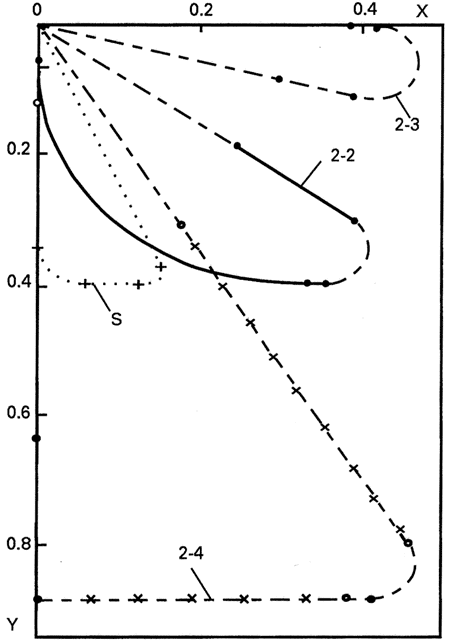Рис.5 - Проекции траекторий аппаратов

Зависимость коэффициента заправочной массы f от числа Маха полета M для АКС-2-2 показана на рис. 6 ломаной линией 2-2. Таким образом, при пространственном выведении полезной нагрузки на орбиту с удалением на юг точки старта второй ступени на расстояние 0.4 L₀ от точки взлета АКС, коэффициент f составит по проведенным оценочным расчетам величину f = 0.39, что на 0.01 больше, чем для аэрокосмического самолета типа Sänger. Отношение массы топлива первой ступени к стартовой массе всего АКС-2-2 составит f₀ = 0.27.

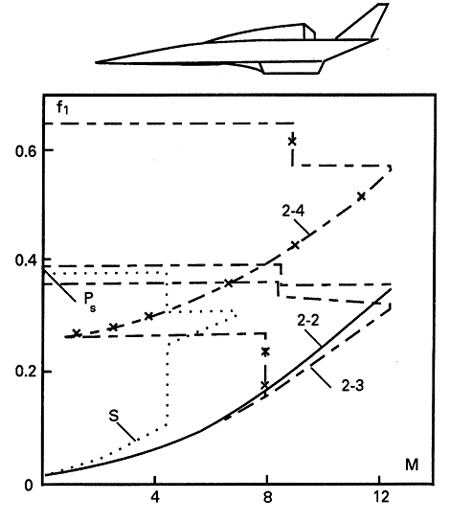Рис.6 - Расход топлива в случае пространственного выведения

Если вернуться к выражениям (5.15) - (5.17), оценить, используя известные параметры траекторий пространственного выведения, увеличение расхода топлива вследствие влияния проекции веса на направление касательной к траектории, и ввести его вместо стандартных потерь в модели первого приближения Δf = 0.02, тогда величина коэффициента заправочной массы f как АКС-2-2, так и аэрокосмического самолета типа Sänger, необходимая для осуществления описанных выше полетов, составит f = 0.39.

Для оценки влияния изменения этого параметра на отношение стартовых масс первой и второй ступеней m₁/m₂ был проведен расчет основных характеристик варианта АКС-2-2, коэффициент заправочной массы которого равен f = 0.38. В этом случае отношение m₁/m₂ = 2.50, то есть при уменьшении коэффициента f на 0.01 и фиксированной массе полезной нагрузки масса первой ступени возрастает в 1.11 раза, а стартовая масса всего аэрокосмического самолета - в 1.08 раза.

При запуске АКС-2 (m₁/m₂ = 2.25) на восток без параллакса наименьшие затраты топлива достигаются при интенсивном разгоне (φ = 1.5, ω = 0.5) по прямолинейной в плане траектории (кривая 2-3 на рис. 5). Для возвращения в точку старта после кабрирования и разделения ступеней необходим разворот почти на 200°, и для того, чтобы при выходе из виража, как и ранее число Маха было равно 8.5, уровень аэродинамического качества K_t должен быть не менее 8.3. При величине K_max = 6.0 это можно обеспечить, если тяга двигателя на вираже в среднем составит 0.28 от сопротивления АКС:

K_t = K_max/(1 - P/X) ( P < X ). (10.5)

Далее следуют короткий участок крейсерского полета и планирование в точку старта. Полная длина полетной дистанции АКС-2-3 будет практически равна номинальной полетной длине L₀, причем около 0.30 дистанции придется на полет без затрат топлива.

Зависимость коэффициента заправочной массы f от числа Маха полета M для АКС-2-3 показана на рис. 6 ломаной линией 2-3. Коэффициент f в этом случае будет равен 0.36 (f₀ = 0.25), что на 0.03 меньше, чем при полете АКС-2-2 на параллакс, равный 3000 км.

Таким образом, предлагаемая схема двухступенчатого аэрокосмического самолета позволяет выводить на низкие околоземные орбиты полезные нагрузки, составляющие 9 - 12 %, и возвращать с орбиты соответственно от 10 % до 0 от его стартовой массы, при радиусе полета на параллакс R₀ = 3000 км. Увеличение относительной массы конструкции первой ступени на 10 % по сравнению со ступенью типа Sänger понизит нижнюю границу доли полезной нагрузки до 8 %.

В заключение следует отметить, что описанные выше "осредненные" траектории использовались только для предварительных оценок основных характеристик рассмотренных схем АКС. Дальнейший более подробный анализ и оптимизация зависящих от скорости полета параметров с учетом их влияния и на массу конструкции аэрокосмического самолета, безусловно, приведет к изменению как формы траектории, так, возможно, и к заметной коррекции некоторых средних величин.

11. Перспективная аэрокосмическая транспортная система

Если увеличивать максимальный радиус полета первой ступени аэрокосмического самолета с целью расширения диапазона углов наклона орбит выводимых им полезных нагрузок, то уменьшается масса груза и при тех полетах, когда большое удаление от точки старта не требуется. Возникает противоречие между гибкостью применения аэрокосмической транспортной системы и ее эффективностью в наиболее типичных случаях.

Это противоречие может быть разрешено применением дозаправки топливом в полете. Однако, дозаправка возможна только на дозвуковых скоростях полета, так как ударные волны, возникающие при движении аппаратов со сверхзвуковыми скоростями, сильно возмущают поле течения, что исключает плавное, точно контролируемое их сближение. Крейсерский полет на достаточно большие расстояния должен совершаться аэрокосмическим самолетом на гиперзвуковой скорости, так как его крейсерские характеристики на дозвуковых скоростях неудовлетворительны. Для дозаправки он должен снизить число Маха полета до 0.7 - 0.8, при этом для повторного разгона до крейсерской скорости потребуется значительное количество топлива. Однако, если учесть, что при высоких значениях K_max затраты энергии в основном преобразуются при планировании в увеличение дальности полета, дозаправка становится целесообразной.

Таким образом, при дозаправке в воздухе криогенным водородом, можно существенно увеличить радиус действия аэрокосмического самолета. В этом случае полностью заправленный АКС-2-2 может совершить полет на юг на расстояние 0.89 L₀, затормозиться до дозвуковой скорости и без потерь развернуться на восток. При M = 0.7 можно произвести дозаправку от ожидающего АКС дозвукового самолета-заправщика, вылетевшего с того же аэродрома, разогнаться по траектории интенсивного разгона, как АКС-2-1, до M = 12.5, совершить маневр разделения ступеней и пространственный разворот с изменениями высоты и скорости полета на 120° без затрат топлива с торможением до M = 9, при этом числе Маха совершить крейсерский полет, а затем планированием вернуться в точку старта (ломаные линии 2-4 на рис. 5 и 6). Коэффициент заправочной массы при дозаправке будет равен f = 0.26 (f₀ = 0.18), радиус действия увеличится более чем в 2.2 раза, и достигнет 6700 км без уменьшения массы выводимой на орбиту полезной нагрузки. При этом выведение полезной нагрузки на экваториальную орбиту становится возможным при широте космодрома не более 60°.

При запуске полезных нагрузок на орбиты с наклонениями не меньшими, чем широта космодрома, а также такими, которые обеспечиваются при полете на параллакс до 3000 км, дозаправка топливом в полете не требуется.

В целом, система, состоящая из двухступенчатых аэрокосмических самолетов и дозвуковых самолетов-заправщиков, может быть чрезвычайно гибкой и в некоторых отношениях существенно более простой, чем флот одних только АКС. При широте космодрома не более 60° и двух дозаправках в воздухе первая ступень АКС может, совершив практически любую мыслимую операцию по выведению полезной нагрузки на низкую орбиту, вернуться в точку старта при коэффициенте f первой ступени не более 0.33 (f₀ = 0.23). Отметим, что две дозаправки АКС в воздухе при определенных условиях можно произвести при помощи одного дозвукового самолета-заправщика.

Боковая дальность при возвращении с орбиты прототипа второй ступени - аэрокосмического аппарата Delta Clipper будет составлять 2500 км [25]. Соответствующий параметр ступени Horus АКС Sänger при движении по некоторой номинальной с монотонно убывающей высотой траектории также равен этой величине [15]. Применение траекторий с рикошетированием, приводящих к периодическому изменению высоты полета, вызывает увеличение боковой дальности полета ступени Horus до величин, существенно превышающих 5000 км [15]. Таким образом, существует реальная возможность сбалансировать дальность полета на параллакс первой ступени аэрокосмического самолета предлагаемой схемы в случае дозаправки в полете и боковую дальность его второй ступени при возвращении из этого полета.

Кроме увеличения радиуса полета в 2.2 раза и уменьшения при двукратной дозаправке отношения массы топлива первой ступени АКС к массе ее конструкции в 1.3 раза, существует и более нетривиальное следствие из применения этой операции. Для его рассмотрения вернемся к выражению (2.1), связывающему коэффициент заправочной массы аппарата f с параметрами f и Δe, характеризующими соответственно относительную тягу его двигателя, набираемую при разгоне удельную энергию, а также пропульсивный коэффициент полезного действия силовой установки (см. п. 2).

Величина параметра Δe для АКС-2 на любом рассмотренном участке разгона не превышает 0.1. В случае линеаризации соотношения (2.1) при Δe << 1 легко получить:

f ~ (1 + 1/φ)/η. (11.1)

Из выражения (11.1) видно, что возможное уменьшение пропульсивной эффективности ГПВРД при максимальных скоростях полета, соответствующее нижней границе значений η(M) на рис. 2, то есть уменьшению этого параметра в 1.3 раза при M = 12.5 по сравнению с принятой в расчетах величиной, может быть компенсировано увеличением тяги двигателя в 1.2 раза (φ = 2) без возрастания расхода топлива на разгонную операцию. При этом только в 1.2 раза уменьшится длина участка разгона аэрокосмического самолета, что имеет значение при полете по траектории типа 2-2, однако при полетах по траекториям типа 2-3 и 2-4 (с дозаправкой) практически не повлияет на основные эксплуатационные характеристики рассматриваемой аэрокосмической транспортной системы.

Итак, аэрокосмическая транспортная система Star Liner, состоящая из двухступенчатого аэрокосмического аппарата с баллистической многоразовой второй ступенью, в котором используются инновации, описанные в п. 7, 8 работы, и дозвукового самолета-заправщика [36] может вывести на низкую околоземную орбиту полезную нагрузку, составляющую 8 - 12 % от стартовой массы АКС, что приблизительно в 8 - 12 раз больше, чем АКС Sänger со ступенью Horus-M, в 4 - 6 раз больше, чем Sänger с беспилотной ступенью Horus-C, или в 6 - 8 раз больше, чем одноступенчатый носитель Delta Clipper. При этом радиус полета предлагаемой аэрокосмической транспортной системы при необходимости может более чем в 2 раза, превышать соответствующий параметр АКС Sänger.

Первая ступень АКС предлагаемой концепции, в отличие от одноступенчатого аэрокосмического самолета, может также стать основой для целой гаммы гиперзвуковых аппаратов, совершающих крейсерский полет в атмосфере при числах Маха от 5 до 10 [23], в том числе для гиперзвукового транспортного самолета с полезной нагрузкой, составляющей 10 % от стартовой массы, и дальностью полета не менее 17500 км.

Следует также отметить, что программа летных исследований, являющаяся одним из необходимых условий превращения предлагаемой концепции в технически обоснованный проект, фактически уже рассматривается в рамках пересматриваемой программы NASP [3,4]. Планы научно-исследовательского центра NASA им. Эймса в настоящее время предусматривают создание пилотируемого экспериментального аппарата HALO (Hypersonic Air Launch Option) с воздушным стартом с самолета-носителя Lockheed SR-71A. Этот аппарат предназначен в первую очередь для решения проблем эксплуатации ГПВРД на режимах полета при М = 9 - 12. Для получения информации о полете в остальной части гиперзвукового диапазона вплоть до орбитальных скоростей (M = 25) предполагается использование беспилотного гиперзвукового летательного аппарата SAPHYRE, запускаемого с помощью одноразовой ракеты-носителя [3,4].

Летные исследования на экспериментальном самолете HYTEX при числах Маха от 0 до 5.6 - 6.8 планируются в рамках немецкой программы Sänger [22]. Испытания аппарата DC-X - демонстратора аэрокосмического носителя Delta Clipper, который является прототипом второй ступени предлагаемой аэрокосмической транспортной системы, должны начаться уже летом 1993 года [37] (первый полет был успешно совершен 18 августа 1993 года).

Таким образом, на основе предлагаемой концепции можно создать многоразовый двухступенчатый аэрокосмический самолет Star Liner со стартовой массой одноразовой ракеты-носителя С. П. Королева "Союз" (m₀ = 310 т, масса полезной нагрузки 7 т, [27]), способный вывести при старте с космодрома на мысе Канаверал на низкую околоземную орбиту с нулевым наклонением полезную нагрузку массой около 30 т, что больше, чем полезная нагрузка частично многоразовой системы Space Shuttle со стартовой массой 2000 т, [27]. С дозаправкой в воздухе, применяя самолет-заправщик типа Ан-124 или Boeing-747F (масса дозаправляемого топлива составит 50 - 55 т), такую транспортную операцию можно осуществить при старте с космодрома Байконур, а при использовании самолета-заправщика типа Ан-225 - даже из Средней Европы или Подмосковья.

12. Заключение

Итак, предлагаемая концепция двухступенчатой аэрокосмической транспортной системы Star Liner при умеренном техническом риске позволяет создать аппарат, способный, по предварительным оценкам, выводить на низкую околоземную орбиту полезные нагрузки, составляющие 8 - 12 % от его стартовой массы, что в 5 - 10 раз больше, чем системы Sänger или Delta Clipper, и возвращать на Землю до 10 % от стартовой массы, при радиусе полета около 3000 км. При этом первая ступень АКС предлагаемой концепции, в отличие от одноступенчатого аэрокосмического самолета, может стать основой для целой гаммы гиперзвуковых аппаратов, совершающих крейсерский полет в атмосфере при числах Маха от 5 до 10. Новые технические решения, касающиеся аэродинамики первой ступени АКС и ее двигательной установки, позволят кардинально улучшить ее основные характеристики и ослабить взаимосвязи между критическими областями технологий, вносящими дополнительные проблемы при ее конструировании.

Рассматриваемые в США и Германии программы проведения летных испытаний гиперзвуковых аппаратов HALO и HYTEX, осуществляемые в России с 1991 года исследования ГПВРД в полете, а также начавшиеся в 1993 году испытания баллистического аппарата DC-X являются полностью адекватной системой исследований в натурных условиях, позволяющей создать технически совершенную и экономически эффективную аэрокосмическую транспортную систему Star Liner.

Включение в предлагаемую аэрокосмическую транспортную систему дозвукового самолета-заправщика обеспечит радиус полета первой ступени более 6500 км и позволит снять практически любые ограничения на углы наклонения орбит выводимых этой транспортной системой полезных нагрузок.

Автор выражает искреннюю благодарность сотрудникам ЦАГИ: В. Е. Денисову, В. И. Бузулуку, Л. Е. Васильеву, А. В. Жданову, В. А. Иринархову, В. Е. Ковалеву, Г. А. Павловцу, С. И. Скоморохову, В. А. Тереховой, Л. П. Федорову и В. Д. Борисову (АНТК им. А. Н. Туполева) за стимулирующие мысль дискуссии и ценные консультации.

Литература

Paige H. W. Lunar Space Transport in 2001. In "Space Age in Fiscal Year 2001", ed. by E. Konecci, M. Hunter II, R. Trapp. An American Astronautical Society Publication, Washington, D. C., 1966.
Williams R. M. National Aero-Space Plane: Technology for America's Future. Aerospace America, vol. 24, N 11, 1986.
Scott W., Kandebo S. NASA-Ames Proposal Could Challenge NASP. Aviation Week & Space Technology, vol. 137, N 11, 1992, p. 27, 30.
Rademacher H. Ritt auf dem Schwarzen Vogel. Flug Revue, N 12, 1992.
Parkinson R. The An-225/Interim Hotol Launch Vehicle. AIAA -91-5006, 1991.
Сообщение ИТАР-ТАСС от 14.12.1992.
Zagainov G. I., Plokhikh V. P., Shkadov L. M., Yaroshevsky V. A. Aerospace Systems Development Directions and Some Aspects of Their Construction and Application. AIAA-90-5266, 1990.
Kors D. L. Design Considerations for Combined Air Breathing-Rocket Propulsion Systems. AIAA-90-5216, 1990.
Künkler H., Kuczera H. Turbo-Ramjet Propulsion System Concept for Future Space Transport (Sänger). Paper IAF-87-265, 1987.
Johnston P. J., Whitehead A. H., Jr., Chapman G. T. Fitting Aerodynamics and Propulsion into the Puzzle. Aerospace America, vol. 25, N 9, 1987.
Tauber M. E., Menees G. P., Adelman H. G. Aerothermodynamics of Transatmospheric Vehicles. J. of Aircraft, vol. 24, N 9, 1987.
Russian Ramjet/Scramjet Operates Successfully. Aviation Week & Space Technology, vol. 137, N 9, 1992, p. 24.
Kandebo S. NASP Gets Go-Ahead to Refine Two-Year Stretchout Program. Aviation Week & Space Technology, vol. 136, N 16, 1992, p. 25.
Jones R., Donaldson C. From Earth to Orbit in a Single Stage. Aerospace America, vol. 25, N 8, 1987.
Koelle D. Sänger Advanced Space Transportation System - Progress Report 1990. AIAA-90-5200, 1990.
Revamping NASP. Aviation Week & Space Technology, vol. 137, N 14, 1992, p. 21.
Asker J. Clinton Offers $15 Billion for NASA with R&D Boost. Aviation Week & Space Technology, vol. 138, N 15, 1993, p. 25, 26.
Левантовский В. И. Механика космического полета в элементарном изложении. М., Наука, 1980.
Henry J. R., Mc Lellan C. H. Air-Breathing Launch Vehicle for Earth-Orbit Shuttle-New Technology and Development Approach. J. of Aircraft, vol. 8, N 5, 1971.
Contensou P., Duban P., Ribaud Y. Moteur a Cycle Inverse (I.C.E.). France, Patent N 2 615 903, 1987.
Hogenauer E. Raumtransporter. Z. Flugwiss. Weltraumforsch., vol. 11, N 6, 1987.
Kuczera H., Sacher P., Krammer P. The German Hypersonic Programme - Status Report 1991. AIAA-91-5001.
Kirkham F. S., Hant J. L. Hypersonic Transport Technology. Acta Astronautica, vol. 4, N 1 - 2, 1977.
Dalby A. R. The Delta Clipper. Ad Astra, vol.3, N 8, 1991.
Colucci F. Launching the Delta Clipper. Space, vol.7, N 6, 1991.
US Standard Atmosphere. Washington, Gov. Print Off., XV, 1962.
Космонавтика (Энциклопедия), под ред. В. П. Глушко. Москва, Советская Энциклопедия, 1985.
Кюхеман Д. Аэродинамическое проектирование самолетов. Москва, "Машиностроение", 1983.
Лобановский Ю. И. Режимы интерференции крыла и корпуса при сверхзвуковых скоростях полета. Ученые записки ЦАГИ, т. 19, N 6, 1988.
Hirschel E. Aerothermodynamics and Propulsion Integration in the Sänger Technology Programme. AIAA-91-5041, 1991.
Minoda M., Sakata K., Tamaki T., Saitoh T., Yasuda A. Feasibility Study of Air-Breathing Turbo-Engines for Horizontal Take-Off and Landing Space Plane. AIAA-89-2296, 1989.
Лобановский Ю. И. Максимальное аэродинамическое качество конических комбинаций крыла и корпуса при больших сверхзвуковых скоростях. Известия АН СССР, МЖГ, N 3, 1983.
Лобановский Ю. И., Нестеров М. Е. Влияние крутки крыла, оптимизированной в рамках гипотезы плоских сечений, на аэродинамические характеристики комбинаций крыла с корпусом при гиперзвуковых скоростях. Ученые записки ЦАГИ, т. 21, N 1, 1990.
Penland J. A., Romeo D. J. Advances in Hypersonic Exploration Capability - Wind Tunnel to Flight Reynolds Number. J. of Aircraft, vol. 8, N 11, 1971.
Ribaud Y. Inverse Cycle Engine for Hypersonic Air-Breathing Propulsion. ISABE 89-7111, 1989.
Лобановский Ю. И. Аэрокосмическая транспортная система. Заявка на патент, Россия, N 93 030 224, 1993.
Lenorovitz M. DC-X to Begin Static Test Firings. Aviation Week & Space Technology, vol. 138, N 20, 1993.

10.10.1993 Ю. И. Лобановский

Концепция перспективной аэрокосмическойтранспортной системы